静态投入产出系统

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第223页（1204字）

将国民经济分为n个生产部门和一个最终需求，部门i的产出x_i中被部门j作为投入吸收的部分记作x_ij，而提供给最终需求的部分则记作y_i，那么投入和产出的平衡可表示为线性方程组

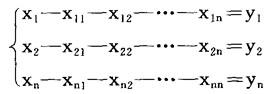
利用投入系数a_ij=x_ij／x_j，方程组可以写成矩阵形式

(I－A)x=y，

其中

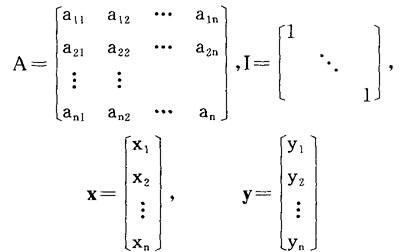
分别为系统的结构矩阵，n阶恒同矩阵，部门产出向量和最终需求向量。

在矩阵I－A满秩的条件下，记其逆矩阵为W=(I－A)^－1，则方程(I－A)x=y的解是

x=Wy

因此，确定对各部门产品的最终需求以后，就可以据此算出各部门的产出应该是多少，这就是经济计划工作。如果在最终需求中把出口作为正分量，进口作为负分量，则上述模型已经把进出口因素包括在内。

来自国民经济统计数据的实际的投入产出结构矩阵A，通常不但使得矩阵I－A满秩，而且使得矩阵W=(I－A)^－1的所有元素非负。

这样，按照x=Wy算出的各部门的产出都非负。通常用公式

(I－A)^－1=I+A+A²+A³+…

计算W=(I－A)^－1。这时，方程

x=Wy=(I+A+A²+A³+…)y=y+Ay+A²y+A³y+…的经济学意义是：当最终需求是y时，总产出不但要包含y，还要包含为产出y所需投入的Ay，为产出Ay所需投入的A(Ay)=A²y，…。

对于实际系统，矩阵级数I+A+A²+A³+…通常收敛得很快，从而只要计算前几项就够了，并且计算是稳定的，经得起数据的扰动。

在开放的亦即把某些部门作为外生部门的投入产出系统中，可以把代表居民总产出x_n+1即总就业水平作为外生变量来处理。当所有内生部门的产出确定之后，总的就业水平将是

X_n+1=a_n+1．1X₁+a_n+1．2X₂+…+a_n+1，nX_n+y_n+1，

其中y_n+1是居民或其他外生部门直接吸收的劳务。

通过平衡方程的各种变形，就可以用投入产出分析方法解决不同的具体问题。