正则经济

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第227页（1123字）

由参数的微小变化只能引起均衡价格的微小变化的经济称为正则经济。

以纯交换经济为例，设经济由m个消费者组成，交换财货n种，第i个消费者由它的初始财货向量e_i和一个可微需求函数f_i表征，i=1，2，…，m。为简单起见，设需求函数不变，只有初始财货量是可变的经济参数。于是，经济E就可看成初始财货向量的m元组(e₁，e₂，…，e_m)。问题是当(e₁，e₂，…，e_m)作微小变化时，E的均衡价格集合是否会发生剧烈的变化。

令p=R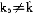(Rⁿ的正卦限)，价格空间为单位单纯形。

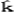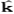S={p=(p₁，p₂，…，p_n)＞0，‖p‖=(p)^1／2=1}。经济E=(e₁，e₂，…，e_m)的超需函数为

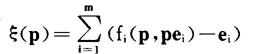
经济E的均衡价格集就是使ξ(p)=0的p的集合。

为了从直观上理解均衡点的集合，设有一个两种财货的经济，由瓦尔拉斯定律知，只要考虑第一种财货的超需ξ₁(p₁)就够了，设p₁∈(0，1)，一般说来，ξ₁(p₁)=0有如下4种可能形式

经济E¹的均衡价格集合由一段区间组成，即均衡价格不是孤立的。E²有一个重根。当参数有微小变化时，这两种情形都要改变它的均衡集的结构(见虚线)。而E³和E⁴则不同，对参数的微小变化，E³仍保持三个孤立的均衡点，E⁴仍保持一个均衡点(见虚线)。由此看出，判断均衡集是否为稳健的，就是看ξ′₁(p)是否为零，在E¹和E²有ξ′₁(p)=0，而在E³和E⁴有ξ′(p)≠0。

从而有定义：设ξ₁(p)是经济E的超需函数，对价格p∈S，如果ξ(p)=0及矩阵[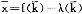ξ₁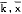，…，ξ_n－1／#p₁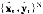，…，p_n－1](p)是满秩的，则称p为E的正则均衡价格。若经济E的所有均衡价格都是正则的，则称它为正则经济。

可以证明，在概率意义下，几乎所有经济都是正则的。

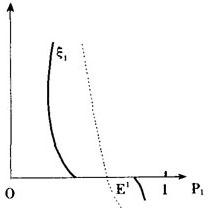
图1

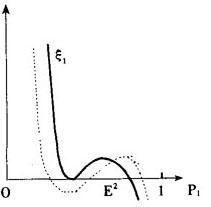
图2

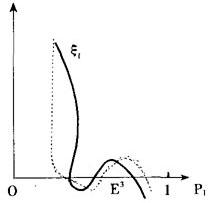
图3

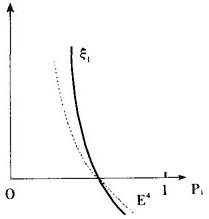
图4