贝叶斯均衡

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第708页（1135字）

贝叶斯均衡是不完全信息博弈(贝叶斯博弈)的均衡概念，静态的不完全信息博弈的均衡被称为贝叶斯纳什均衡，动态的不完全信息博弈的均衡被称为精炼的贝叶斯纳什均衡。

解决不完全信息的方法是使用哈萨尼转换(参见哈萨尼转换)。

静态贝叶斯博弈记为G={a₁，…，a_n；θ₁，…，θ_n；p₁，…，p_n；u₁，…，u_n}。其中a_i是第i个博弈方采取的行动(纯策略)，a_i∈A_i(θ_i)，A_i(θ_i)是第i个博弈方类型依存的行动空间；θ_i是第i个博弈方的类型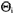，_i是第i个博弈方的类型空间；p_i是第i个博弈方的类型为θ_i(θ_i∈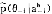_i)的概率。

u_i是第i个博弈方的效用，u_i=u_i(a₁，…，a_i，…，a_n；θ₁，…，θ_i，…，θ_n)=u_i(a_i，a_－i；θ_i，θ_－i)。其中θ_－i=(θ₁，…，θ_i－1，θ_i+1，…，θ_n)。

定义一：如果对所有的i，a_i^*∈A_i(θ_i)，使得：

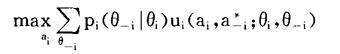
则a^*=(a₁^*，…，a_n^*)就称为一个(纯策略)贝叶斯纳什均衡。

混合策略的贝叶斯纳什均衡的定义类似。其中p_i(θ_－i|θ_i)是第i个博弈方在已知自己的类型为θ_i时判定其他博弈方类型属于θ_－i的概率。

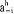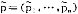在动态博弈中，记S_i(θ_i)为第i个博弈方类型依存的策略空间，s_i∈S_i(θ_i)是S_i中的一个特定的策略。记a_i=(a，…，a#₁，a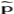₊₁，…，a)是在第h个信息集(参见信息集)上参与人i观测到其他参与人的行动组合。

记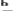(θ_－i|a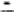_i)是第i个博弈方在观测到a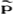_i后关于θ_－i的后验概率。

定义二：精炼贝叶斯均衡是一个策略组合s^*=(s₁^*，…，s_n^*)和一个后验概率分布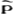=(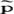₁，…，_n)，满足：

1．对于所有博弈方i，在每一个信息集h，s_i^*使得：

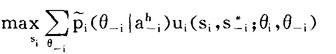
2．后验概率_i(θ_i|a_i)是使用贝叶斯法则，从先验概率p_i(θ_－i|θ_i)，观察到的a_i和最优策略s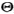_i得到的(在可能的情况下)。

需要注意的是，精炼的贝叶斯均衡不仅仅是关于策略的均衡，而是关于策略s^*和对类型的判断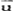(信念)的共同均衡。给定信念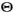，策略s^*是最优的；给定均衡策略s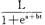^*，是使用贝叶斯法则从均衡策略和观测到的行动得到的。