税收累积：概念、测定与减轻

出处：按学科分类—经济 经济科学出版社《公共经济学大辞典》第482页（10468字）

【内容介绍】：

1．引言

每当一种商品或服务在经过生产－分配链条的各个阶段(比如从制造阶段到零售阶段)上某种税不只课征一次时，就出现了税收累积问题。

引起税收累积的典型税种就是多阶段一般流转税(multi－stage general turnover tax)，有人也称之为总收入税(gross receiptstax)或交易税(transaction tax)(Due，1988)。在课征这种税的情况下，每次销售交易都要课税，其税率或依阶段的不同，或交易的不同，或两者兼有而不同。

例如，对橡胶的销售课征x%，而对轮胎销售课征y%；由于橡胶的价值体现在轮胎的价值中，所以橡胶被课征了两次税；如果再考虑到从轮胎制造商那里购买轮胎的批发商要纳税z%，那么，这种税就不只课了两次。从上面的描述中我们很容易看到，对一种课税商品或服务所课征的累积税的有效税收负担，在这些商品或服务到达最终消费者手中时，可能要比这种税在消费者购买的阶段所明确规定的名义税率高得多。换言之，即使一种商品或服务在零售阶段被免了税，但它的价格中也很可能会包含着以前阶段生产中的各种投入要素所被课征的各种税收因素。因此，消费者通常看不到累积税的实际负担。

普遍一致的看法是：累积课税不理想，因为对最终消费前的各阶段的交易征税所导致的经济扭曲，要比只对最终消费一个环节征税高得多，如零售税和扩大到零售阶段的完全成熟的增加税。当然，按统一税率课征的一般累积税不会导致生产过程中最适要素比例选择的扭曲，但可能导致经济中产业组织的过度纵向合并。

在尚未以非累积税取代累积税之前，也有多种机制可以减轻税收累积的程度。

2．税收累积的概念

销售税一般有两种类型：单阶段销售税和多阶段销售税。

单阶段销售税只在生产－分配链条的一个阶段上征收，诸如它可能只对制造、批发或零售阶段的销售征收。相反，多阶段销售税在生产－分配链条的几个阶段上征收，诸如流转税和增值税。

这些税种可能会对经济中商品和服务的大部分销售征收，而不管这种销售处于生产－分配链条中的哪个阶段。

税收累积是由于在生产－分配链条的某一阶段上对来源于前一阶段的征了税的增值额课税所致。在多阶段零售－流转税下，对所有的销售都要征税，对投入物已经纳税的企业没有任何抵免。

如果对生产－分配链条中的每个阶段的销售都征税就会产生税收累积(McMorran，1995，p．80－82)。

我们举一个数字例子来说明了生产－分配链条中四个阶段的销售按10%征收多阶段流转税所产生的税收累积。在第一阶段，最初的生产者向制造商销售100元。该生产者的增值额是100元，而且该销售的10%的税收主要是针对该阶段的增值额。在第二阶段，制造商销售给批发商210元。

制造商的购进额包括税收在内为110元，增值额是100元。在销售时，制造商一共交了21元的税收，其中10元是当前阶段的增值额的税额，10元是以前阶段的增值额的税额，而1元是以前阶段对销售课征的税收的税额。在第三阶段，批发商销售给零售商331元。零售商的购进额包括税收在内为231元，增值额是100元。

对销售课征的税收是33．1元，其中10元是当前阶段的增值额的税额，20元是以前阶段的增值额的税额，3．1是以前阶段对销售课征的税收的税额。在第四阶段，零售商销售给消费者464．1元。零售商的购进包括税收在内是364．1元，增值额是100元。对这笔销售课征的税收是46．41元，其中10元是当前阶段的增值额的税额，30元是以前阶段的增值额的税额，6．41元是以前阶段对销售课征的税收的税额。

3．税收累积程度的决定因素

税收累积的实际负担落在最终消费者上的程度，取决于大量复杂的、交织在一起的因素，本节讨论其中的一些比较重要的因素。

3．1 需求弹性与供给弹性

众所周知，生产者把其产品的税收负担转嫁给购买者的能力，取决于相关的需求弹性和供给弹性。

在只有一种课税商品的局部均衡框架中，这种弹性的结果有四种不同的组合，图1的四个图形所示。在每一个图示中，DD′是需求曲线，SS′是税前供给曲线，TT是税后供给曲线。在每一价格水平P上，SS与TT之间的垂直距离等于τP，这里τ是从价计征的税率。如果P₀和P₁分别代表税前和税后均衡价格水平，那么，从图1中很容易看出，征税后价格水平的上升程度取决于需求曲线与供给曲线的特定形状(在图1中的符号△代表任一变量的变动)。

倘若需求曲线是垂直的(图1a)，即需求弹性为零，或供给曲线是水平的(图1d)，即供给弹性为无穷大，这种税就会全部被向前转嫁，即购买者承担全部税收负担，因为价格水平与税率的提高比率相同。如果需求曲线是水平的(图1c)，就不会有任何前转。

在大多数情况下，即需求曲线和供给曲线不呈现极端的弹性，税收负担会发生部分前转(图1b)。

从图1中可以看出，这种税对课税商品的价格和需求数量都有影响，继而会影响到其他商品(甚至是不课税的商品)。

因此，不进行一般均衡分析，就不能确定这种税前转的最终程度。已有大量文献讨论了税收(可计算)一般均衡效应(Shoven and Whalley，1972，p．281－321)。

不过，对间接税经济影响的大多数政策分析中，通常是以短期的、局部均衡为重点，在这种情况下，比较合适的假设是：间接税的全部前转首先发生(如图1d所示)。

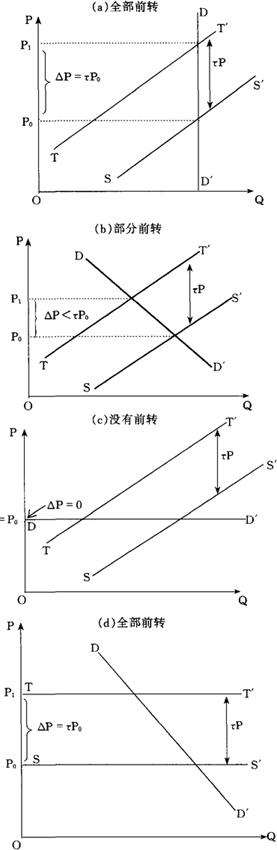
图1 供求弹性与税收负担转嫁

3．2 征税与不征税投入物的比率

在生产－分配链条上的每个阶段，生产者价格中所包含的税收负担的大小，取决于在该阶段的征税与不征税投入物的比率以及该比率在以前阶段的状况。

这些比率越低，税收负担就越小。例如，在许多发展中国家，食品价格所包含的税收成分通常相对较低，因为大多数国家在食品生产中使用的农业投入免税。

3．3 价格累加的程度

在任何一个既定的生产或分配阶段上，当销售者把其产品价格提高到超过其投入物的税收负担时，就会出现价格累加(price pyramiding)。例如，如果他具有一定的垄断力量，并且在税收增加时能够从事这类增加其额外利润的定价行为，就会出现这种情况。

3．4 生产－分配链条中的阶段数量

一种商品在到达消费者手中之前所经过的生产和分配阶段越多，投入物被重复征税的次数就越多，从而产生的税收累积程度也就越高。

在实践中，分析一种特定商品的价格中所包含的税收累积程度，通常很难清理出上述因素间的相互关系。

不过，有些简单的解析方法可以用来系统研究这一问题(Zee，1995，p．75－79)。

4．税收累积的简单解析分析

4．1 单一生产－分配阶段的税收负担转嫁

令p代表一种商品的生产者价格，k代表每单位产出的投入物成本，v代表商品的每单位增值，τ代表应税投入物的从价税率，γ代表征税投入物占总投入物的比例。这样，我们利用公式分析就可以得出：

p=v+k(1+γτ) (1)

我们把变量δ定义为增值额占投入物的含税成本的比率，即

δ=v／［k(1+γτ)］ (2)

利用(2)式，(1)式可改写成：

p=k(1+γτ)(1+δ) (3)

因此，δ可以看作是投入物的含税成本的加价比率。如果投入物的不含税成本(k)保持不变，那么从(2)式中可知，加价比率的任何比例变动都是因为增值额的比例变动超过税率的比例变动所引起的，也就是说，

△δ／δ=△v／v－γ△τ／(1+γτ) (4)

(4)式在描述生产者的定价行为时至关重要。

为了证明这一点，我们首先把φ定义为是p对τ的弹性：

φ=(△p／p)／［γ△τ／(1+γτ)］ (5)

也就是说，φ计算的是τ变动1%所导致的p变动的百分比。但是，如果直接依据(3)式，p的比例变动为：

△p／p=γ△τ／(1+γτ)+△δ／(1+δ) (6)

因此，通过把(6)式替代到(5)式，φ就可以重新表示为：

φ=1+(△δ／△τ)［(1+γτ)／γ(1+δ)］ (7)

(7)式表明，φ的关键决定因素是表达式(△δ／△τ)，它计算的是加价比率δ对税率τ变动的反应；这种反应又取决于愿意让其产出的增值额变动［如(4)式所示］的程度。

下面就其中的两种基准情况进行分析。

4．2 情况A：充分价格累加(△δ=0)

如果生产者不允许其加价比率变动，即△δ=0，那么依据(7)式马上可以得出φ=1，因而税率提高1%将导致这种产品价格足额上升1%，与征税投入物－不征税投入物比率和征税投入物－增值额比率无关。

从事这类定价行为的生产者，其增值额显然会因税收的变动而增加。

从(4)式中的确可以看出，当△δ=0时，增值额的比例变动等于税率的比例变动。

4．3 情况B：税收负担没有转嫁(△v=－γk△τ)

由于某些原因，倘若生产者完全不能向前转嫁其税收负担［例如他所面对的需求曲线是水平的，如图1(c)所示］，那么，任何税收变动的归宿都会全部落到他的增值额上，即△v=－γk△τ。把它代入到(4)式，可以看到该生产者的加价比率变动由下式给定：

△δ=－△τγ(1+δ)／(1+γτ) (8)

根据(7)式，我们可以得到φ=0；也就是说，生产者的价格p不变。

这一结果仍然与γ无关。

上述两种情况显然包容了生产者价格对税率变动的所有可能的反应。

一种令人感兴趣的中间情况是：生产者在面对税收变动时，只保护他的增值额(△v=0)。在这种情况下，根据(4)式，生产者的加价比率的变动是：

△δ=－△τδγ／(1+γτ)

把该表达式代入(7)式，得到：

φ=1／(1+δ)＜1

因此，生产者价格的比例变动是正的，但小于税率的比例变动；而且由于δ的大小与k和γ逆相关［如(2)所示］，所以，征税投入物－不征税投入物比率和征税投入物－增值额比率越高，价格变动的幅度越大。

4．4 综合性规则

在不同的税收负担转嫁程度的假设下，模拟分析用一种税替代另一种税对价格产生的影响是很有益的。为此，倘若包括上述两种情况在内的所有可能的生产者价格变动都能通过改变一个参数来表现，那么分析起来就非常方便。达到这一目的的最简单的程序就是把定价机制概念化，依据的不是(1)式，而是下列综合性规则：

p=A(1+ατ) (9)

式中，1≥α≥0，A是非零常数。

因此，这种充分价格累加情况意味着α=1，而没有税收负担转嫁情况意味着α=0。

在0到1之间改变α就可以囊括所有可能的结果，包括上面所讨论的中间情况，即生产者定价行为使其增值额不受税收变动的影响。

4．5 税收累积与生产和分配的多阶段

在多阶段生产和分配的情况下，在每个阶段，生产者的定价行为(可能不同)、税率、征税投入物－不征税投入物比率以及征税投入物－增值额比率，都将与税收累积对消费者面临的价格的最终影响有关。因此，上面的有关单阶段的解析分析不能简单地推广到多阶段情况中。不过，在特殊的假设条件下，即所有生产者都将从事充分价格累加行为，可以阐示一种令人感兴趣的基准情况。

下面的分析所使用的符号含义不变，只是用下角标来代表不同的阶段。在第一阶段，生产者的定价行为由下式给定：

p₁=(1+τ₁)k₁(1+δ₁) (10)

式中，k₁代表生产者购买的投入物，按税率τ₁征税，δ₁是该生产者的加价比率。

因此，在α=1和A=k₁(1+δ₁)的情况下，(10)式与(18)式给出的综合规则相对应。作为在第一阶段生产者的产品的购买者，在第二阶段生产者按生产者价格p₁购买其投入物，即

k₂=p₁

如果这些投入物按税率τ₂课税，那么该生产者就会根据下式确定其价格：

p₂=(1+τ₂)k₂(1+δ₂)

=(1+τ₂)p₁(1+δ₂) (11)

利用(1)式，把(2)式重新写成：

p₂=(1+τ₁)(1+τ₂)(1+δ₁)(1+δ₂)k₁ (12)

(3)式可以一种简单的方式就能使其通用于任何阶段数量。如果p_n是n阶段后的生产者价格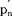，代表没有税收情况下的相应生产者价格，那么这二者间的比率可测定生产者价格的税收累积程度。根据(12)式，可以推断该比率是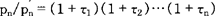： (13)

在所有税率都相同的特殊情况下(如单一税率的一般流转税)，τ₁=τ₂=…=τ_n=τ，(13)式可以采取下列简化形式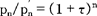： (14)

当然，一种税也可能是在生产－分配链条的最后阶段之后对最终消费者征收。

如果p_c代表含税价格(这种税是按税率τ_c对消费者课征的)，那么，在n阶段之后，消费者价格将是：

p_c=(1+τ_c)p_n (15)

按定义，对处于该链条之末的最终消费者所课征的τ_c的影响，没有余地再向前累积了。

4．6 综合性规则

我们在生产者充分价格累加行为这种特殊假设情况下，对多阶段的情况进行了解析分析。

但是，这种假设对税收累积的程度设了一个上限。如果一些生产者从事不充分价格累加的行为，那么由此导致的多环节的程度就要比(13)式或统一税率情况下的(14)式所表明的程度低。倘若税率实际上是统一的，就这种多阶段情况而言，通过一个简单的综合定价规则也可能得到这一结果，类似于(9)式给定的单阶段情况。

不管生产－分配链条中的阶段数量有多少，按统一税率τ课征的一般流转税对消费者价格的影响都可以用下列综合性规则说明：

p_c=B(1+βτ)(1+τ) (16)

式中，B是非零的常数，β(≥0)是到达最终消费者之前在各个阶段根据生产者的定价行为向前累积的税收负担总量。

如果β=0，在该生产－分配链条中没有生产者向前转嫁其税收负担，因此也就不会有税收累积。β的上限用β^*表示，代表充分价格累加行为的结果，它取决于生产－分配链条中的阶段数量。根据(14)式，很容易看出β^*由下式给定：

β^*=［(1+τ)ⁿ－1］／τ (17)

因此，通过在0到β^*间改变β的值，就可以模拟出所有可能的税收累积程度的影响。例如，如果n=2，并且每个生产者都从事充分价格累加行为，那么，通过把(17)代入到(16)式，消费者价格将是：

p_c=B(1+τ)³ (18)

其中，假定

B=p₂=(1+δ₁)(1+δ₂)k₁。

5．税收累积程度的估计

模拟分析税收累积对消费者价格的影响对于比较不同税种的价格效应大有裨益，除此之外，对某种现行税种的税收累积程度进行经验估计有时也很必要。一般说来，在没有我们前面所说的那些关于税收累积的所有决定因素的详细信息的情况下，这种估计很难进行。不过，倘若某种现行税种是统一税率，(16)式给定的综合定价规则就可以依据几个通常可以找到的收入和支出总体数据推导出β的估计值。

令E和E′分别代表不含税的征税与不征税最终消费支出总额。

如果对资本和中间产品课征的所有税种被认为通过不同程度的税收累积最终落在消费上的，那么根据综合定价规则，可得：

R=［(1+βτ)(1+τ)－1］E+βτE (19)

式中，R代表税收收入总额。(19)式右边的第二项代表在最终消费点上未征税消费支出部分所包含的累积税收数量。然而，E和E不能直接观察到，因为消费数据一般都是含税的。如果F和F′分别代表可观察到的征税与不征税的最终消费支出，那么，E和E就可以推导出来：

E=F／［(1+βτ)(1+τ)］ (20)

E=F／(1+βτ) (21)

把(20)式和(21)式代入到(19)式，就可以解出β：

β=｛R－F［τ／(1+τ)］｝／τ(F+F－R) (22)

(22)式是一个简单而直接的公式，可以一来估计统一税率的任何税种的累积程度

6．减轻税收累积的机制

税收累积可能会导致相对价格的扭曲，因为不同商品和服务的最后销售的有效税率与法定税率不同。

当资本投入物存在税收累积时，可能还会导致企业的资本成本增加，扭曲生产效率。有许多机制可以减轻销售税的税收累积的产生的不良后果。

6．1 单阶段销售税

为了消除单阶段销售税下的税收累积，注册的贸易者之间的销售通常不征销售税，即注册的卖主向未注册的购买者销售以前不征税，这就是为什么单阶段销售税有时被称为暂停性税收(suspensive taxes)的原因。

这种税实质上保护了那些正在生产或交易应税产品的企业，消除了那些企业从其他应税生产者和交易者那里购买的税收。

在实践中，卖主的义务就是要向税务机关证明他的某些特定销售无需纳税。在正常情况下，税务机关会接受购买者的注册号和其他信息，如企业名称和地点以及足以证明该卖主无需对其销售纳税的证据。

从表面上看，无论是对政府还是对企业，这种暂停机制似乎简便易行，但事实并非此。这样制度可能会产生滥用或不服从。

供给者必须评估购买者提供给他们的证据，而购买者有可能向供给者提供虚假的证据。

这种机制的更为根本的问题是不能完全消除税收累积，因为只对注册的生产者或交易者减免税。如果生产或分配链条的某些部分在税收上不允许注册，就会产生税收累积。常见的例子就是对进口品和制成品课征的、但对批发和零售或初级产品不征税的单阶段制造商销售税。

在这种情况下，最初生产者可能会使用在制造或进口阶段应税的投入物生产产品。如果这些产品接下来被制造商或进口商用于生产应税产品，那么在这种生产－分配链条的前一阶段已征税的增值额还要被征税，从而导致税收累积。

6．2 多阶段销售税

从本质上看，流转税是累积税，因为在生产－分配链条的许多阶段都要征税而没有任何减除生产投入物课税的机制。

有些国家试图允许减除某些生产投入物的税收来减轻流转税的税收累积，这通常是通过允许企业对一些特定项目的缴纳的税收进行抵免来实现。这些项目包括资本购买或进入生产过程的其他投入物。

部分减免确实在一定程度上消除了流转税制中的税收累积，但并没有完全消除税收累积。

有些国家利用部分减免作为抵免机制的一种试验方法，向引入增值税迈进。

多阶段非累积性税或增值税是交易者对每个阶段的增值额支付净税额的税种。基本方法有两种。

第一种方法是发票抵免法(credit－invoice method)，即在确定应向税务当局缴纳的净税额时，允许交易者在其销售的应纳税额中抵免其购买已缴纳的税额。

第二种方法是减法(subtraction method)，即要求交易者按销售与购买的投入物间的差额计算增值额，并免除按此差额计算的税收。

发票抵免制是增值税的一个主要优点。

它提供了一个查账的证据，使得税收管理更加容易，而且鼓励了自愿缴纳这种税。这种机制也优于暂停机制。但是，如果存在免税，发票抵免机制也不能完全消除税收累积。

只购买应税投入物的应税企业所计算的净税额，是其销售税额与其购买已付税额之间的差额，即企业增值额的税额。

但是，如果该企业还购买了一些免税投入物，那么它的免税购买就没有税额，这些购买也就不能申请抵免。因此，净税额就是企业增值额的税额加上免税投入物的税额。

免税投入物的价值等于该生产－分配链条中所有以前阶段的那些免税投入物的增值额之和。如果这些增值额中有些在以前被征过税，那么就会存在税收累积。

增值税(Value－Added Tax)

Due, J. F., 1988, Indirect Taxation in Developing Economics, Johns Hopkins University Press.

McMorran, R. T., 1995, Mechanisms to Alleviate Cascading, in P. Shome, ed., Tax Policy Handbook, IMF.

Shoven, J. B. and J. Whalley, 1972, A General Equilibrium Calculation of the Effects of Differential Taxation of Income from Capital in the U. S., Journal of Public Economics 1.

Zee, H. H., 1995, Tax Cascading: Concept and Measurement, in P. Shome, ed., Tax Policy Handbook, IMF.