税收归宿的一般均衡分析
出处：按学科分类—经济 经济科学出版社《公共经济学大辞典》第507页（19606字）
【内容介绍】：
税收变化的一般均衡分析明确地把因税收变化而引起的所有市场(包括商品市场和要素市场)上的价格和数量变化都考虑进来。
在现实经济生活中，由于存在着大量的市场，这种分析可能是一个艰巨的任务。为了分析，必须对经济是由数目可控的商品和要素市场所构成的现实世界予以抽象。可以证明，若仅限于经济是由两种商品、两种生产要素组成的，就可以看清税收变化的一般均衡归宿。这种研究税收归宿的理论方法，最早是由哈伯格(Har-berger，1962，p．215－240)创立的，后为米兹克沃斯基(Mieszkowski，1967，p．250－262；Mieszkowski，1969，p．1103－1124)、布瑞克(Break，1974，p．119－240)以及小麦克卢尔(McClure，1975，p．125－161)等完善与发展。
这里使用的模型与讨论最适竞争性价格体系所用的模型相同，有关两部门静态新古典一般均衡模型的分析，可参阅琼斯(Jones，1965，p．557－572)、约翰逊(Johnson，1971)、卡夫斯和琼斯(CavesandJones，1973)以及鲍德威(Boadway，1979，ch．1)等的着述。本文根据鲍德威(boadway，1979，p．299－323)的分析，首先以两部门一般均衡模型对税收归宿理论进行图解(KrauseandJohnson，1972，p．357－382)，然后将以传统的代数方法分析同样的问题，最后用凯恩斯学派的短期模型分析税收归宿。
1．一般均衡税收归宿分析：几何方法
1．1 两部门一般均衡模型的假设条件
首先，回顾一下两部门一般均衡模型中的特定假设，并增加为分析税收归宿所增加的假设。这些假设条件概括如下：
第一，经济具有两种可利用的生产要素：劳动力(L)和资本(K)。这些要素的服务可按竞争性市场上决定的价格w(工资率)和r(租金率)来购买。在课税的情况下，这些要素价格可能依据不同的用途而有所变化。
第二，生产要素L和K可以通过价格体系配置给X和Y这两种商品的生产。每一行业雇佣劳动力和资本在既定的技术条件下生产产品，该技术状况可用等产量图(如图1所示)来说明。
假定每一行业的生产都表现为规模收益不变，也就是说，劳动和资本投入的按比例增加将引起产量按比例提高，而且在边际技术替代率(MRTS)递减的情况下，劳动力和资本彼此可以替代。竞争性条件保证：要素价格比率或工资－租金比率(w／r)，等于边际技术替代率。
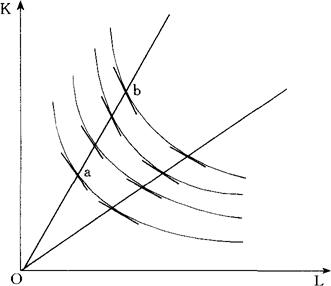
图1 等产量线
第三，假定每一行业的等产量线是齐次的。
齐次性可由图1的等产量图来说明。
如果所有等产量线的斜率沿着从原点出发的射线保持不变，就可以说等产量线是齐次的。由于每条从原点出发的射线都与特定的资本－劳动比率相关(也就是说，K／L=射线的斜率)，劳动与资本间的MRTS以及因此工资－租金比率，将惟一与既定的资本－劳动比率有关，而与产量水平无关。
特别地，当资本－劳动比率提高时，工资－租金比率也提高。等产量线的曲率决定对K／L变化做出反应的工资－租金比率变化的程度；反之，亦然。
把资本－劳动比率变化的百分比除以租金－工资比率变化的百分比作为替代弹性σ：
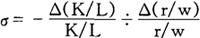
或以微分表示的点替代弹性是：
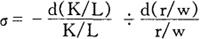
等产量线越平直(亦即它的曲率小)，替代弹性σ越大。
如果等产量线是直线，则σ取无限值；如果等产量线不存在替代性，故成直角形，则σ取零值。
一般来说，σ在等产量线上的不同点取不同的值，但为了简化起见，时常假定它在整个等产量图中是常数。倘若如此，生产函数属于“不变替代弹性”(CES)型生产函数(Arrow，Chenery，Minhas，and Solow，1961，p．225－250)。
当σ=1时，就会出现CES生产函数的特例。也就是说，科布－道格拉斯生产函数可以写成：
X=ALαK1－α
式中，A是规模比例参数，α是小于1的常量。
实际上，可以证明，α是产出中的劳动份额，1－α则是资本份额。在替代弹性为1的情况下，这些份额是不变的。
这是因为，依据上述方程式，当σ=1时，rK／wL是不变的。
最后需要指出的是，既是齐次的，又表现出规模收益不变的生产函数称为线性齐次生产函数(linear homogeneous prOduction function)。
在图1中，如果Ob=K·Oa，即如果生产函数是线性齐次的，这意味着，在b点的产量等于K乘以在a点的产量。
第四，X和Y这两个行业可能具有不同的替代弹性值σ，并在相同的工资－租金比率上展现出不同的资本－劳动比率。在任何既定的工资－租金比率上具有较高的K／L的那个行业称之为资本密集型行业。
另一个行业就是劳动密集型行业。
第五，劳动力和资本得到充分利用，并且各行业是完全流动的。除了特殊说明之外，一般假定劳动和资本的供给是固定的。
这意味着，可以埃奇沃斯方框图(Edgeworth box)表明该经济的生产可能性(production possibilities)。根据埃奇沃斯方框图中的契约曲线(contract curve)，可以推导出生产可能性曲线(如图2所示)。
第六，无论在什么情况下，都涉及到给公共部门转移资源的数量相同的两种税相互替代问题。
在所有情况下，假定政府需要一定数量的劳动力和资本。
所要考察的是剩下的L和K是如何由价格机制来配置的，以及当用于为政府支出融资的税收类型变化时，那种资源配置是如何变化的。换言之，这种分析属于差别税收归宿。
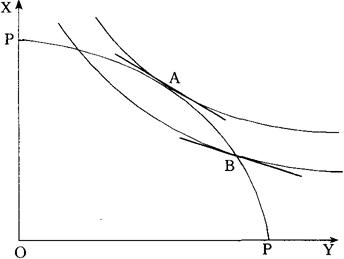
图2 生产可能性曲线
第七，就需求方面而言，该模型最简单的修正是把整个经济归并于一个需求函数中。在该需求函数中，对每种商品的需求取决于所得和相对产品价格。
鉴于税收变化的差别归宿性质，故所得项通常被忽略。既然税收变化的前后，私人部门可利用的资源数量相同，税后所得几乎是不变的，因此，就可以集中分析相对价格变化(不考虑所得变化)所导致的需求变化。在更为一般的模型中，对奢侈品和必需品这两种商品的需求具有不同需求函数的所得集团可以有许多。
第八，商品和生产要素的价格是这样的价格，使所有市场上的需求等于供给。
在这个模型中，主要研究四种类型的税收：特定商品税、一般消费税或所得税(在这个没有储蓄的模型中，一般商品课税等同于一般所得税，因为全部所得都花费在消费品上)、一般要素税以及部分要素税。下面，利用几何分析方法，尽可能地分析这些税的一般均衡归宿。
1．2 一般均衡税收归宿分析：图解
特定商品税 首先考察这样一种简单的情况：要素供给是固定的。
利用图2中的生产可能性曲线PP，分析对X商品课征的税取代产生相同收入的一次总付税。曲线PP表明的是在公共部门的需要已得到满足的情况下，私人部门可利用的X和Y的组合。当利用一次总付税时，经济达到诸如A点，在该点，MRTXY=MRSXY。
现在，假定所有人的嗜好都一样，所得都相同，因而这样画的无差异曲线与个人消费者的无差异曲线相同。当对所有人的影响都一样的一次总付税被一种对X商品课征的税种(税率为tX)所取代时，经济移动到B点，在该点，对消费者来说，X的相对价格已提高，而对生产来说，X的相对价格已下降，从而，
MRSXy=pX(1+tX)／pY
=(1+tX)MRTXY
为了确定MRTXY的下降对相对要素价格的影响，利用埃奇沃斯方框图，如图3所示。根据微观经济学知识可知，图3中契约曲线上的每一点都相应于图2中的生产可能性曲线PP上的点。PP上的同样的两个点A和B在连接OX和OY两点的契约曲线上表现出来。在A点，租金－工资比率由X和Y的等产量线的公共斜率(common slope)给定，用(r／w)A表示。需要注意的是，在A点，X行业所使用的劳动与资本的比率——LX／KX，是OXA直线的斜率。
同样地，LY／KY比率是OYA直线的斜率。由于此图是这样画的，故在A点以及所有沿该契约曲线的其他点，LX／KX＞LY／KY。因此，X行业是劳动密集型行业，Y行业是资本密集型行业。倘若该契约曲线是对角线，则X行业和Y行业中的要素集约度可能是相等的(LXKX=LY／KY)。
倘若该契约曲线偏向东南角，则Y行业可能是劳动密集型行业，而X行业可能是资本密集型行业。
对X课税之后，生产从A点重新配置到B点。
这种变化值得注意的一点是这两个行业的劳动－资本比率都提高了。由于劳动和资本是从X行业释放出来的，而X行业每单位资本利用的劳动力比Y行业的相对多，那么，为了使所有要素都得到利用，劳动－资本比率在这两个行业必须得到提高。
随着这两个行业的劳动－资本比率的提高，MRTSKL或r／w也提高。同劳动力的价格相比，资本价格的相对提高将引致企业通过提高其劳动与资本的比率而节省资本使用。
因此，在从A点向B点的运动过程中，r／w比率也一定会提高，直至所有劳动力和资本都得到充分利用为止。因此，
(r／w)B＞(r／w)A
这表明，相对来说，如果X行业是劳动密集型的，对X行业课税将引起r／w提高。
同样的分析将表明，相对来说，如果X行业是资本密集型的，r／w将下降。更一般地说，这一结果可作如下表述：对某一行业的产出课税，将引起该课税行业中使用密集度高的那种要素的相对价格下降。
根据图2和图3可以推断，r／w的变化程度取决于下列因素：
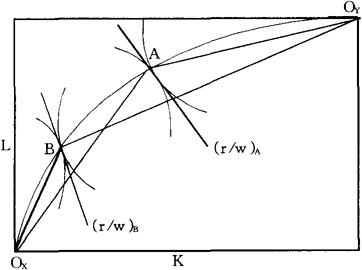
图3 埃奇沃斯方框图
第一，要素比差异。L／K的差异越大，每一行业在从A点向B点的运动过程中，它的变化越大，因而r／w的变化越大。
第二，X的需求弹性。X的需求弹性越大，从Y到X的需求的重新配置越大，因而r／w的变化越大。
第三，X和Y中的替代弹性。在X和Y中，L替代K的替代弹性越小，等产量线的曲率越大，因而要素比率变化所导致的r／w的变化越大。
上述分析表明了，对由相同的人构成的经济中的X课税，将导致商品和要素的相对价格是怎样变化的。
现在，假定在该经济中有许多不同的人，他们当中的每个人对X和Y的偏好都是不同的，而且每个人都拥有不同数量的劳动力和资本。同比如说对全部所得课征非扭曲税相比，这种税仍然把需求从X转向Y。这种需求转移对相对要素价格的影响将如上所分析的那样。
同比例所得税相比，消费税将对从课税行业中集约使用的要素上获得大量(相对而言)所得的人造成伤害(因为他的相对报酬下降)。相反，在税收变化之后，从未课税行业中集约使用的要素上获得高比例所得的人福利将提高。
从家庭预算的使用方面来看，个人对这两种商品消费的比例不同。对于那些其预算中X所占份额较大的人来说，这种税的负担相对重一些(即将减少更多的福利)。
例如，如果X是奢侈品，其需求收入弹性大于1，这种税的负担更多是由高收入的人承担。
最后，简单地深入探讨一下要素供给不是固定的而是变动的影响。
例如，假定要素供给随着工资率的变化而变化。如果X是劳动密集型行业，对X课税可能引起工资率下降。工资率的下降被将来的劳动供给减少缓和了。整个经济的L／K比率下降，这种税对r／w的影响降低。同理，如果X是资本密集型的行业，这种税可能降低r／w，从而引起劳动供给增加。劳动供给的增加将提高经济中的L／K比率，因而减轻r／w的下降。
在任何一种情况下，这种税的变化对劳动力的收益产生的有利或不利的影响，由于劳动供给的变动性而被减轻。
一般消费税 现在，考察一下以相同的税率对X和Y课税。在劳动供给和资本供给是固定的经济中，这种税是一种一次总付税，因为它等同于对固定要素所得征税。
经济中的每个成员按其所得(或消费)的比例承担这种税。在单一消费者或若干相同消费者的经济中，一般消费税可能不影响相对价格、资源配置或效用水平。
在那种个人的嗜好或所得不同的经济中，情况就不是这样了。
例如，想像一下用一般所得税(在此没有扭曲效应)取代对所有人的课税额都相同的一次总付税或人头税的情况。这两种税都是有效率的，但同获取相同收入的人头税相比，所得税将增加低所得者的所得，减少高所得者的所得。如果高所得者和低所得者的偏好不同，这种纯收入再分配将引起资源的重新配置。
如果X比Y的收入弹性高，税收变化将降低X的需求，而提高Y的需求。
在X的生产中集约使用的要素的相对要素价格将下降，恰与上述特定商品税的情况一样。
如果要素供给是变动的，对所得课征的一般税将不再是中性的。
这种税将减少来自供给生产要素的报酬，从而要素供给会发生变化。例如，如果劳动供给与工资率呈正向变化但资本供给是固定的，那么，一般所得税可能减少劳动供给，降低经济中的L／K比率，从而提高w／r。劳动力所有者可能成功地把其一部分税收负担转嫁资本所有者。
如果资本供给是变动，情况就会相反。
一般要素税 现在，考察比如说对劳动所得课征的一般要素税(工薪税)的情况。在仅有一个消费者、要素供给固定的经济中，这种分析仍然是简单的。
对固定要素(劳动力)的课税，将全部由劳动所得承担，因为这是一次总付税。资源配置或相对价格不会发生变化。
在有许多不同的消费者的经济中，用劳动所得课税取代产生相同收入的一次总付税，表明对劳动力的所得进行纯再分配。劳动所得的收入者最为偏好的商品，其需求可能要下降。
资源可能要从这种商品上转移出去，在其生产过程中相对集约使用的要素可能获得相对较低的报酬。
当被课税的要素的供给是变化的时，一般要素税就不再是一次总付税了。
例如，对劳动所得课征的工薪税，将降低供给劳动的收益，引起劳动供给下降。这将引起整个经济的L／K比率下降，导致企业支付的w／r比率提高。实际上，劳动力所有者一直能够部分避免这种税的负担，转嫁到资本身上，途径是减少他们的劳动供给。
从家庭预算的使用方面来看，对劳动所得征税将引起劳动密集型行业生产的那种商品的相对价格提高，这是因为在劳动密集型行业的生产总成本中，劳动力成本所占的比重相对较大。
因此，劳动力所有者不仅通过降低L／K比率而把部分税收负担转嫁给资本所有者，而且他们还把部分税收负担转嫁给在其预算中劳动密集型商品占更大比重的那些人。
劳动力所有者转嫁税负的能力取决于下列因素：
第一，劳动力的供给弹性。劳动供给的弹性越大，转嫁程度越大。
第二，X和Y中的替代弹性。
替代弹性越低，在L／K的变化一定的情况下，w／r的变化越大。
第三，劳动密集型商品的需求弹性越低，这种商品的需求者承担的税负越多。
部分要素税 对某一行业中的某一种要素的使用征税是最复杂的一种税，因为它引起经济中的生产低效率，从而经济处于生产可能性曲线之下运行。例如，考察一种以税率tKX对X行业中的资本课征的税。
当X属于公司部门，Y属于非公司部门时，这种税可能被认为是公司所得税。为了便于几何分析，假定要素供给是固定的。
这就可以利用图4所示的埃奇沃斯方框图来说明既定的劳动力和资本存量在这两个行业间的可能配置。
图4 部分要素税的归宿
在征收一次总付税情况下，经济将在充分效率情况下运行。
沿契约曲线可能达到某一点，诸如A点。在这一点上，MRTXY=MRSXY。在A点，这两个行业的租金－工资比率(r／w)A等于MRTSKL。现在，用对X中的资本课税取代一次总付税。
可以预期，将会出现以下两种情况：
第一，由于X中的某一种要素投入被课税，相对于Y而言，X的价格将提高。这可能引起需求从X转移到Y，资源就可能从行业X重新配置到Y行业。
第二，对KX征税破坏了生产效率条件，因为：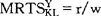
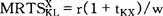
由于税后资本收益在这两个行业中一定是相同的，则结果确实如此；否则，资本所有者就会有一种刺激，促使他把资本重新配置于收益率较高的行业。因此，Y行业的资本收益r，也一定是X行业的税后收益，所以，r(1+tKX)是税前收益或边际产品价值。
由于MRTSKL在X行业和Y行业是不同的，则L和K的配置将不在契约曲线上。假定B是在课征部分要素税的情况下所获得的新的均衡生产点。在B点，同A点相比，X的生产正在下降，而Y的生产正在增加，而且生产是无效率的。
在分析部分资本税的归宿时，因相对价格变化引起的产出从X重新配置于Y与由此产生的无效率导致的脱离契约曲线的运动，在概念上予以区别开来是有意的。
用米兹考茨基(Mieszkowski，1967，p．250－262)的术语，前者称之为产出效应(output effect)，后者称之为要素替代效应(factor substitution effect)。下面考察每一效应如何影响劳动力和资本的相对价格(r／w)。
产出效应(output effect)是指在不考虑生产低效率的情况下，资源从X重新配置到Y对(r／w)的影响。如果X是劳动密集型的(如图4所示)，L和K从X重新配置到Y可能引起(r／w)提高，因为X所释放的L与K的比率，大于Y目前的L与K的比率。
相对资本而言，劳动力不是稀缺的，其相对价格降低。
如果课税行业X是资本密集型的，相反的情形可能存在，产出效应会使(r／w)趋于下降。因此，对KX课税的产出效应，其作用可能有利于也可能不利于资本所有者，这要视X是劳动密集型行业还是资本密集型行业而定。
要素替代效应(factorsubstitution effect)是指由于对资本市场的扭曲而导致偏离契约曲线向B运动。
起初，税收的影响是减少X行业的资本收益。资本所有者因此而把资本从X中抽出来投入到Y中。
这引起X的K／L比率降低，Y的K／L比率提高，所以，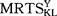
下降，而
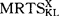上升。资本的这种运动将持续下去，直至整个经济的(r／w)下降到使得MRTS
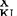=r(1+tKX)／w以及
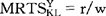为止。
同产出效应不同，要素替代效应对r／w的影响是明确的。它引起r／w下降，从而可能对资本所有者不利(相对于劳动力所有者而言)。
税收对r／w的总体影响取决于产出效应和要素替代效应的综合强度：
第一，如果X行业是资本密集型的，这两种效应将使r／w下降。人们可以预期，公司部门比非公司部门的资本密集程度高，在这种情况下，产出效应和要素替代效应可能使资本所有者的福利下降。
比如说，同对要素所得课征的一次总付税相比，资本所有者的福利可能下降，劳动力所有者的福利可能提高。
如果产出效应非常强，r／w下降的程度可能大于rtKX，则同对资本所得课征一般要素税的情况(全部由资本承担)相比，资本所有者的福利可能下降。
第二，如果X行业是劳动密集型的，产出效应和要素替代效应的作用相反。对r／w课税的影响取决于这两种效应的相对强度。
如果它们正好相互抵消，r／w不会变化，tKX的归宿将与对资本和劳动所得课征的一般所得税相同。实际上，资本已成功地把部分税收负担转嫁给了劳动力。当课税后，r／w提高甚至也是可能的。如果X行业的劳动密集程度很高，产出效应非常大，这种情况可能会发生。同对所有所得课征一般税相比，若对X行业的资本课税，资本所有者的福利可能会提高。
r／w的变化程度也将取决于该经济的需求和生产的特点。
下面把各种参数对r／w变化的影响加以概括：
第一，X的需求弹性越大，产出效应对r／w的影响程度越大。这是因为，从X到Y的资源重新配置程度越大。
第二，X和Y的K／L比率差额越大，产出效应越大。
第三，X的生产成本中，资本的份额越大，产出效应越大，因为pX／pY的变化将越大。
第四，X和Y的替代弹性越小，产出效应越大。因为对于每一行业中的L／K的变化是既定的来说，r／w的变化更大。
第五，X的替代弹性越大，要素替代弹性越大。如果在X中，L和K的替代性相当高，则当LX／KX变化时，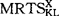
不会变化很大，以致于大部分税收影响是降低r／w而不是提高r(1+tKX)／w。
2．一般均衡税收归宿分析：代数方法
2．1 两部门一般均衡模型方程组的建立
下面的分析是建立在米兹考茨基(Mieszkowski，1967，p．250－262)的分析基础上，使哈伯格(Harberger，1962，p．215－240)早期的税收归宿分析更加精炼和一般化。分析这样一种最简单的情况：要素是固定的，只有一种囊括所有消费者以及政府的总体需求函数。
依据上述这些经济学家的观点，假定政府花费税收收入的方式恰与消费者支出方式相同。依据下列分类——供给、需求、市场清卖、定价等，构建一般均衡体系方程式。
这种分析是比较静态分析，所有方程式都以微分变化而非绝对值来表示。
供给 基本供给关系式是生产函数。
对于X行业而言，可写作：
X=f(LX，KX) (1)
对该方程式全微分，得到：
dX=fLdLX+fKdKX (2)
式中fL和fK是劳动力和资本的边际产品，即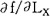
和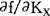
。依据竞争性假设，要素报酬等于边际产品价值(即wX=pXfL)。用这个关系式除以X，把(2)式转化为：
X′=θLXL′X+θKXK′X (3)
式中，“′”代表比例变化(即X=dX／X)，θLX是X的生产成本中的劳动份额(θLX=wXLx／pxX)，θKX是成本中的资本份额(θKX=rxKx／pXX)。由于假定生产函数是线性齐次的，要素报酬恰好用光产品价值，所以，θLX+θKX=1。
也就是说，pXX=wXLX+rXKX。用pxX来除此式，得到：θLX+θKX=1。
对于Y行业，虽然可以推导出类似于(3)式的方程式，但可以证明，在该体系中不一定需要它。
［关于这一点的技术原因说明如下。
根据瓦尔拉法则，如果一般均衡体系中的所有预算限制都得到满足，如果除了一个市场之外，所有市场都是清卖的(供给等于需求)，那么，这最后的一个市场也必然是清卖的。这意味着：在分析这种体系的均衡或均衡中的变化时，可以省去一个市场清卖条件。
在这个体系中，省去的是Y的市场清卖条件，所以无需担心它们的需求或供给条件。如果X、L、K的市场都是清卖的，则根据瓦尔拉法则，Y的市场也一定是清卖的。
关于以简单的一般均衡模型对瓦尔拉法则的阐示，参见韩德森和匡特(Henderson and Quant，1958)］所需要的其他供给关系是σx和σY的替代弹性。σx的值可以作如下定义：
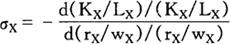
式中，rX和wX分别是X行业中的资本与劳动力的毛收益。
对分子和分母求导，上述表达式变成：
K′X－L′X=－σX(r′X－w′X) (4)
同样地，σY的表达式成为：
K′Y－L′Y=－σY(r′Y－w′Y) (5)
需求 X的基本需求方程式，一般来说是下列形式：
X=X(L，pX，pY) (6)
式中I是所得。由于需求函数在所有价格和所得中都是零齐次的，故只有相对价格才是重要的。
而且，由于所得变化可以不必考虑(因为政府花费税收收入的方式与消费者的支出方式相同)，故这个需求方程式通常可简化为：
X=X(pX／pY) (7)
对(7)式微分，并通过除以X而把它转化为变化率，则以比例变化表示的X的需求成为：
X′=E(p′X－p′Y) (8)
式中E近似为X需求的补偿相对价格弹性。近似地说，此项是插入项，因为假定不存在收入效应，不考虑因课税而造成的超额负担。
为了看清这一点，考察图5描述的对X课征消费税的情况。在征税之前，经济处于A点，产量是X1。对X商品课征消费税，并把其收入一次性分配，使经济沿生产可能性曲线移动至B点，这时，产量为X2，新的一组相对价格为pX／pY。补偿性需求弹性表明的是，如果消费者仍处于相同的无差异曲线上，pX／pY变化所引起的X的需求变化。在这种情况下，消费者可能达到C点，消费数量是X3。由于课税的超额负担，消费者的效用减少了，新的相对价格只能在B点获得，这时的需求数量是X2。
只有当无差异曲线在纵向上是平行的时，X2和X3才是相同的。因此，包括在方程式(8)中的适当的弹性E实际上是在生产可能性曲线上X关于pX／pY的需求弹性(Bailey，1954，p．255－261)，而不是补偿性弹性。就部分要素税而言，这种分析还要复杂些，因为税后B点位于生产可能性曲线之内。在下面的分析中，利用的是E的修正后的解释。
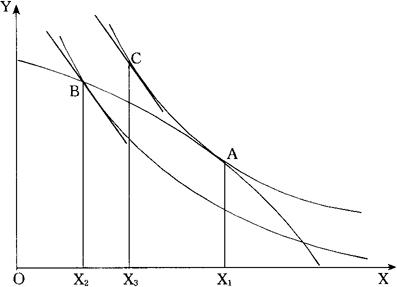
图5 对X课征消费税的归宿
市场清卖条件 本模型假设所有要素都得到充分利用，以至于在这两个行业中，每一要素都必须用光。K和L的市场清卖条件是：
KX+KY=K* (9)
LX+LY=L* (10)
式中，K*和L*是各要素的既定供给。
对这些市场清卖条件式进行全微分，得到：
dKX=－dKY (11)
dLX=－dLY (12)
X的市场清卖已经隐含在该分析中，因为在以方程式(3)和(8)表示的供给和需求关系式中所用的X的数量相同。
定价方程式 px的定价方程式根据投入和产出价值相等条件求得：
pXX=wXLX+rXKX (13)
对这个方程式全微分，得到：
pXdX+XdpX=wXdLX+rXdKX+LXdwX+KXdrX
然而，根据对X的生产函数(1)式全微分，得到：
dX=fLdLX+fKdKX
上式两边同乘以pX，得到：
pXdX=pXfLdLX+pXfKdKX
依据利润最大化的边际生产力条件，可得：
pXdX=wXdLX+rXdKX
因此，用上式减去这个方程式，得到：
XdpX=LXdwX+KXdrX
或者，以比例变化方式重写这个方程式，即：
p′X=θ′LXw′X+θKXr′X (14)
式中，w′x和r′x是X行业中的毛要素报酬的变化。
假定对X行业的资本按从价税率TKX课税。于是，该经济中的资本净收益r与rX的关系是：
r=rY=rX(1－TKX) (15)如果对该表达式进行微分，并假定dTKX=TKX，以至于开始时这种税是零，得到：
r′=r′X－TKX (16)
在对LX或X不征税的情况下，定价方程式是：
p′X=θ′LXw′+θKX(r′+TKX) (17)
同样地，就pY′而言，若假定对Y行业不征税，得到：
pY′=θ′LYw′+θ′KYr′ (18)
2．2 两部门模型的代数分析
至此，已有8个方程式，即(3)式～(5)式、(8)式、(11)式～(12)式、(17)式～(18)式等，而未知数是九个，即(X′，p′X，p′Y，r′，w′，K′X，L′X，K′Y，L′Y)，因而这个方程式体系不能求解。但是，由于该方程式体系只能对相对价格求解，故可以取消一个未知数。从技术上说，该方程式体系在价格上是零齐次的，因而把所有价格(pX，pY，w，r)都增加1倍对资源配置绝对不会有影响。
因此，价格水平可以任意选择，最简单的方法是任意地确定某一个价格为1。
假定让w=1，所以，w′=0；也就是说，劳动力是计价物(numeraire)，所有价格都以劳动单位来表示。在未知数中取消w，这样就剩下了8个未知数和8个方程式。由于所有方程式都是线性的，利用矩阵代数方法，求得以该模型的外生变量(θ，E，σX，σY，TKX)表示的每一个未知数。
为了说明该解的性质，求出r′的解。由于劳动力是计价物，r′是租金－工资比率的比例性变化。通过整理上述方程式，r′的解是(Mieszkowski，1967，p．250－262；Shoven and Whalley，1972，p．281－321)：
r′=［(θKXA+B)／D］TKX (19)
其中，
A=E(KX／KY－LX／LY)
B=－σX(θLXKX／KY+θKXLX／LY)
D=E(θKY－θKX)(KX／KY－LX／LY)+σY+σX(θLXKX／KY)+θKXLX／LY
为了解释这个结果，首先要注意是，分母D总是正的。这是因为E总是负的。另外，在以没有税收的情况开始时，θKY－θKX总是与KX／KY－LX／LY的符号相反。这一结论直接来自θKX和θLX的定义。
如果KX／LX＜KY／LY(若X是劳动密集型的)，则分子中的第一项是正的；如果KX／LX＞KY／LY(若X是资本密集型的)，则分子中的第一项是负的。分子中的第一项恰是上一节所说的产出效应。若X是资本密集型行业，要素从X行业移出，将有害于资本。需要指出的是，E的绝对值越大，X的需求弹性越大，产出效应越大。这反映出，这种弹性越大，征税所导致的从X转移到Y的资源越多。
方程式(19)中的第二项B总是负的，因为σX＞0。
它对应于要素替代弹性。X的替代弹性越大，对r的降低效应越大。
在这种情况下，资本不能把税负转嫁出去。
如果r′=0，当征税时，整个经济的租金－工资比率保持不变。
税收负担按照要素对GNP的贡献比例，落在每一要素所得上。这意味着，资本成功地把一部分负担转嫁给劳动力。
如果r′＜0，资本承担的税收负担比例，大于它对GNP的贡献比例；反之，亦然。根据方程式(19)，TKX对r的影响是不明确的，除非X是资本密集型的。
倘若如此，r′＜0以及资本将承担的税负比例大于它对GNP的贡献比例；也就是说，在这种情况下承担的税负比例高于在一般所得税情况下承担的税负比例。
根据上述分析，按税率TLX对X行业的劳动力课征部分要素税对r′的影响可以表述如下：
r′=［(θLXA－B)／D］TXL (20)
式中的A、B、D项同上述定义。
这里，税收落在资本上的比例明确地低于若X是劳动密集型行业情况下的比例(r′＞0)。
若按相同的税率(TXL=TKL)把这两部分要素税合并在一起，其结果等同于对X课征特定商品税。
根据方程式(19)和(20)，得到：
r′=(A／D)TX (21)
没有发生要素替代效应，而且，当X是资本密集型行业(A＞0)时，资本承担的税负比例大于它对GNP的贡献比例；反之，情况相反。
3．税收归宿分析的凯恩斯短期模型
这里，短期是指资本存量是既定的。为了简化起见，劳动力存量也是固定的，但在各工厂间是变化的。在下面分析的模型中，假定：第一，设备和劳动力都是充分就业的；第二，技术与具有倒L型供给曲线的每类设备成固定比例。
这两个假设使得每一设备在其供给曲线的纵向部分上运行，而且当经济变化时，劳动力和设备不会改变。在L型供给曲线和劳动力在企业间的分配是既定的情况下，整个经济的产出由下列方程式给定：
O=aL (22)
式中，O是总产出，L是劳动供给，a是整个经济的产出－劳动比率。在充分就业的情况下，O是一定的。产出既可能用于消费(C)、总投资(I)，也可能用于政府支出(G)，所以，
O=C+I+G (23)
凯恩斯学派的短期分析的关键假设是：投资是固定的(Kalecki，1937，p．444－450)。
根据方程式(23)，O和G是固定的意味着总消费也是固定的。
于是，分析变成总消费如何在社会各“阶级”间分配。这里，把社会阶级划分为两部分，即食利阶层和工人阶层。工人阶层的货币所得来源于固定的货币工资。
在假定工人阶层把其全部所得都消费掉的简单情况下，他们的实际所得取决于产品的相对价格。
假定定价是以成本加成方法确定的。价格是在平均变动成本之上加入一特定百分比λ，因此，
p=(1+λ)w／a (24)
w和a都是固定的，但λ可以调整，以便使基本的市场清卖等式成立，保证储蓄等于投资(S=pI)。
食利阶层的所得来源于每一企业的工资加价。
当课征消费税时，消费者的价格由下式给定：
p′=(1+tc)p (25)
货币GNP既可以用产出价值的总和来表示，也可以用生产要素的报酬总和来表示。因此，
p′C+pI+pG=wL+π+tcpC+pD (26)
式中，π代表的是利润(税前扣除折旧的利润)，D代表的是实际折旧支出(它是固定的)。
把方程式(22)～(25)代入方程式(26)，得到把必要的毛利率λ与实际利润水平(π／p)相联系起来的方程式：
［λ／(1+λ)］aL=π／p+D (27)
毛利越高，实际利润就越高，因为a、L、D都是固定的。
这种分析可以用来说明差别归宿。
假定政府支出水平是固定的，分析以一种税替代另一种税(二者的税收收入相同)的效应。政府的预算限制式是：
pG=twwL+tfπ+tr(1－tf)βπ+tcpC (28)
式中，tw是对劳动所得的课税，tf是对利润的课税，tr是对食利阶层所得的课税，β是分配给食利阶层的利润比例。对保留收益不征个人税。
在凯恩斯学派模型中，满足基本均衡的条件是储蓄等于投资。
由于投资是固定的，则该体系就要通过调整毛利来实现满足既定投资所需要的利润数额。满足总投资需要的储蓄来源于以下三个来源：折旧、企业的保留收益、食利阶层的储蓄，用公式来表达，即：
S=pl
=(1－tf)π［(1－β)+s(1－tr)β］pD (29)
式中，s是食利阶层所得的储蓄倾向。由于D和I是固定的，根据方程式(27)就很容易看出，该经济中的基本平衡机制是与毛利λ有关的实际利润水平π／p。
用p除方程式(29)，则方程式(29)可以改写成下式：
(1－tf)π／p［(1－β)+s(1－tr)β］
=I－D (30)
方程式(27)和(30)是决定毛利λ和实际利润水平π／p的充分条件。
根据这些方程式，可以对差别税收归宿做出如下推断：
第一，假定提高tf(利润税)而降低tw(工薪税)，以便使G的水平不变。根据方程式(30)，无论tr是否不变，(1－tf)π／p肯定是不变的。
因此，食利阶层的实际所得(1－tf)(π／p)β是不变的，他们的消费也是不变的。这样，工人阶层的消费不变意味着：利润税和工资税以相同的方式筹措税收收入。当tf、π／p提高，从而λ也提高时，将会发生什么情况?毛利越高意味着对工人阶层来说价格越高，但这将被他们适用的低税率tw所抵消。
可见，以利润税取代产生等额收入的工资税，将使劳动力的福利提高，提高的程度等于这种税的税额。
第二，当以任何税收取代tr时，工人阶层的福利下降，而食利阶层的福利提高。这种变化总是使食利阶层的消费增加。
根据方程式(30)，tr下降一定伴随着(1－tf)(π／p)提高。因此，食利阶层的实际所得(1－tf)(π／p)β一定提高，因而他们的消费也一定会提高。
第三，在保持预算平衡的情况下提高G和税收，将使工人阶层的福利下降(这忽略了政府支出增加可能给工人阶层带来的任何利益)。
这将降低包括工人阶层可利用的消费总量(C)。
上述简单地说明了随着模型的假定变化，税收归宿的结果是如何变化的。这里表明的凯恩斯学派模型的结果关键取决于如下两个假定：即投资水平是固定的，支出比例是固定的。
因此，该模型能否最佳地描述现实，还是个经验问题。
【参考文献】：
税收转嫁与归宿(Tax Shifting and Incidence)
税收归宿的局部均衡分析(Partail Equilibrium Analysis of Tax Incidence)
税收归宿的静态一般均衡分析：历史发展(Static General Equilibrium Analysis of Tax Incidence：The Historical Development)
Arrow, K. J., H. B. Chenery, B. S. Minhas, and R. M. Solow, 1961, Capital-Labor Substitution and Economic Efficiency, Review of Economics and Statistics 43.
Bailey, M. J., 1954, The Marshallian Demand Cure, Journal of Political Economy 62.
Boadway, R. W., 1979, Public Sector Economics, Massachusetts: Winthrop Publishers,Inc. .
Break, G. F., 1974, The Incidence and Economic Effects of Taxation, in The Economics of Public Finance, Washington: The Brookings Institution.
Caves, R. E. and R. W. Jones, 1973, World Trade and Payments, Boston: Little,Brown and Co. .
Harberger, A. C., 1962, The Incidence of the Corporation Income Tax, Journal of Political Economy 70.
Henderson, J. M. and R. E. Quant, 1958, Microeconomic Theory: A Mathematical Approach, New York: McGraw-Hill.
Johnson, H. G, 1971, The Two Sector Model of General Equilibrium, Chicago: Aldine-Aiherton Press.
Jones, R. W., 1965, The Structure of General Equilibrium Models, Journal of Political Economy 73.
Kalecki, M., 1937, A Theory of Commodity, Income and Capital Taxation, Economic Journal 47.
Krause, M. B. and H. G. Johnson, 1972, The Theory of Tax Incidence: A Diagrammatic Analysis, Economica.
McClure, Jr. , C. E., 1975, General Equilibrium Incidence Analysis: The Harberger Model after Ten Years, Journal of Public Economics 4.
Mieszkowski, P. M., 1967, On the Theory of Tax Incidence, Journal of Political Economy 75.
Mieszkowski, P. M., 1969, Tax Incidence Theory: The Effects of Tax on the Distribution of Income, Journal of Economic Literature 7.
Shoven, J. R. and J. Whalley, 1972, A General Equilibrium Calculation of the Effects of Differential Taxation of Income from Capital in the U. S., Journal of Public Economics 1.