财政乘数

出处：按学科分类—经济 经济科学出版社《公共经济学大辞典》第1052页（16377字）

【内容介绍】：

乘数(multiplier)是一种宏观的经济效应，也是一种宏观经济控制手段，是西方经济学家研究经济波动时应用的一种概念性工具。

它由英国经济学家R．F．凯恩(Kahn，1931，p．173－198)于1931年在其《国内投资对于失业的关系》一文中首先提出来的。当时，他研究了投资变动对就业量增加的影响。但有些西方经济学家指出，凯恩是乘数理论的发明者，只是在开始给予精确的数学公式这个意义上是正确的。后来，凯恩斯对这一概念加以利用，用来研究投资变动对总收入的倍增作用。

按照凯恩斯的说法，乘数是指投资增加时，会引起收入增加，而收入的增加将是若干倍于投资量，这个倍数就是乘数。所以，乘数是指投资与收入在量上的关系。

但凯恩斯这里所说的投资和收入，不是指投资后带来的利润，而是指投资形成的购买，由购买所形成的社会收入。可见，乘数是支出(买)→收入(售)→支出(买)……连锁反应的概括和定量化表述。

以后，西方经济学家根据这一基本概念，提出了许多专门的乘数，如对外贸易乘数，它研究不断变化的进口量的作用；又如连续周期乘数，研究乘数作用的时间选择问题。财政政策乘数研究财政收支变化对国民收入的影响作用，其中包括财政支出乘数、税收乘数和平衡预算乘数。

1．国民收入决定模型

国民收入决定理论是推导和理解财政乘数的基础。为了分析简便，先不以具有国际经济的封闭性经济为前提，而且不考虑公司利润留存、国有企业和财产收入等因素。

财政支出只用于购买当期产品，税收也只是所得税。另外，价格水平在短期内不受总需求变化的影响。

在上述假设条件下，把下列五个方程式作为国民收入的决定模型，并以此为依据作进一步考察。

Y=C+I+G (1)

C=a+c(Y－T) (2)

I=e+h(Y－T) (3)

G=G′ (4)

T=b+tY (5)

(1)式是收入决定模型中的第一个基本方程式。

其中，Y表示生产(等于分配)的国民收入，C、I和G分别表示民间消费支出、净民间投资支出以及政府在产品和劳务方面的支出。但这与国民收入的核算不同，这些变量都是事先的计划量，因而，(C+I+G)不外乎是国民支出的计划额。

所以，需要注意的是，(1)式已不是恒等式。(2)式至(4)式，均表示国民支出的三个组成部分的决定式。

在上述条件下，求导国民收入均衡值是极为容易的。先将(5)式的T值代入(2)式和(3)式，得到：

C=a－bc+c(1－t)Y (6)

I=e－bh+h(1－t)Y (7)

在这两式中，Y的系数c(1－t)和h(1－t)表明的是在税率表一定的情况下，Y每增加一个单位，C和I所增加的比例，即dC／dY和dI／dY。

西方经济学家分别把它们称之为“国民收入的边际消费倾向”和“国民收入的边际投资倾向”，并将这两者之和命名为“国民收入的边际支出倾向”，用符号F表示。

接下来，把(6)式和(7)式中的C和I之值以及(4)式中的G值，一同代入决定国民收入的基本方程式(1)式中，则：

Y=a+e+G′－b(c+h)+FY (8)

因此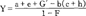， (9)

其中，

F=(c+h)(1－t)

从(9)式中可以看出，无论何时，政府支出和民间支出都会存在，所以，不管Y怎样降低，这两种支出都会维持较大的正值。

故此，(9)式的分子一般来说应是正值。这样，为了使均衡国民收入保持正值，必须保证F＜1。由于在一般情况下，0＜t＜1，而可支配收入的边际支出倾向(c+h)一般也是小于1的，所以，0＜F＜1存在。

从(9)式可知，均衡国民收入取决于a、e、G′、c、h、b和t这些参数值。

如果这些参数值发生变化，均衡国民收入Y就会变动。这里所要研究的，正是财政当局能够操纵的变量(政策变数)G′、b、t在变动时，Y的均衡值会受到影响的程度，即财政乘数。

2．财政支出乘数

推导 财政支出乘数指因政府支出的增加(减少)所引起的国民生产总值或国民收入增加(减少)的倍数。由于从性质上看，政府支出包括转移性支出和耗竭性(消耗资源的)支出，因此，财政支出乘数可分为转移性支出乘数(transfer expenditure multipiler)和耗竭性支出乘数(exhaustive expenditure multipiler)。

现假定购买性(耗竭性)支出发生变化，由G₀′变为G₁′，随之，国民收入由Y₀变成Y₁。如果G′－G₀′=△G′，Y₁－Y₀=△Y，则根据(9)式，可以推导出下列关系式：

或者，

△Y=△G′／(1－F) (10′)

(10′)式更清楚地说明，财政支出变化引起国民收入变化多少。从这个意义上说，(10)式即可称为“财政支出乘数”。这个乘数就是1减去国民收入的边际支出倾向的倒数。

根据0＜F＜1这样的假定，乘数值大于1。它的经济意义在于，财政支出的单独增加或减少，会使国民收入以更大的速度上升或下降。所以，政府支出政策具有稳定(或反周期)经济发展的潜力。

之所以会有这样的结果，是因为财政支出的增加将提高国民收入水平，然后再通过可支配收入增加，刺激民间支出的增加。

这种作用随着F值的大小而增减。可见，财政支出乘数的值会随着下列三种情况而变大：(1)可支配收入的边际消费倾向c增大；(2)可支配收入的边际投资倾向h增大；(3)实际边际税率t降低。

需要注意的几个问题 第一，这里所说的财政支出是指政府在购买商品和劳务方面发生的支出。类似于社会保障支出的转移性支付，其乘数效应一般比购买商品和劳务支出的乘数效应弱，除非社会保障金的领取者把这部分收入全部用于支出。

政府用于贷款和偿还债务的支出，一般情况下与商品和劳务购买支出的乘数相同。为什么耗竭性支出乘数的乘数效应可能大于转移性支出乘数?这是因为耗竭性支出的变化不会引起储蓄变化(政府的边际消费倾向等于1)，而转移性支出变化所导致的民间部门的支出变化要受到整个社会的边际储蓄倾向的制约(Herber，1971，p．474)。

换言之，第一轮的耗竭性支出是国民生产总值的直接组成部分，而第一轮的转移性支出仅仅是购买力的转移，其中有一部分购买力在进入支出流之前被储蓄起来。所以，耗竭性支出乘数没有这种初始的“储蓄渗漏”(saving leakage)。

第二，假定财政支出全部用来购买本期商品和劳务。如果用于购买像土地、建筑物等资产，只要卖方不将其全部收入用于投资支出或消费支出，财政支出的乘数效应就会减小。

第三，这里假定税率不变。实际上，政府支出的变动常常伴随着其他参数的相应变动。

而G′和b或t的同时变动对△Y的影响是一个更为复杂的问题，这将在分析平衡预算乘数时探讨。

第四，利用(9)式计算自发决定的投资或消费的乘数，它们与财政支出乘数一致，即：

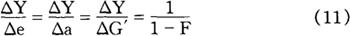
西方经济学家把1／(1－F)称为“支出乘数”，而其中的△Y／△e一般称为“投资乘数”［在这个模式中，如果假设t=0，h=0，就能得到凯恩斯《通论》中所给出的投资乘数：1／(1－c)］。

这两种乘数的值之所以一致，是因为不仅有已提到的几个假设，而且还由于因政府支出而获得收入的人们，其边际支出倾向与经济整体的平均水平相等。特殊的情形是，在救济性公共事业支出的情况下，由于收入获得者的最初边际支出倾向一般都格外高，故财政支出乘数要大于1／(1－F)，并超过民间投资乘数值。

第五，在经济繁荣时期，财政支出增加对实际收入的影响能力出现减弱趋势。因为在这种经济状况下，财政支出扩张将导致国民支出增加，这会刺激价格水平上升，从而对实际国民收入的增长来说，其作用不大。

第六，财政支出乘数效应受利率的影响。在国民收入提高时，出于交易目的的货币需求会增大；在货币供给不变的情况下，一般都是利率上升。

利率的这种变化会抑制民间投资。因而，财政支出的扩张效应在一定程度上被抵消。

第七，财政支出的增加一般要使货币量和公债规模发生变化，并通过对利率和货币资产的影响，从而对民间消费和民间投资产生间接影响。

财政支出政策与财政状况 下面分析财政支出的单独变化对财政结余(S_g=T－G)的影响。

在上述模式中，T=b+tY，G=G′。所以，

S_g=b+tY－G′ (12)

(12)式的两边同除以G′。

得到：

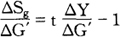
将(10)式所表明的财政支出乘数值代入此式，得到：

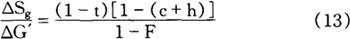
只要假定c+h＜1，(13)式的值就一定是负值，而且其绝对值小于1。可见，财政支出的增加一定会使财政收支恶化，而盈余的减少额或赤字的增加额则小于支出的增加额。其原因是存在“相互抵消效应”，即税收会随着国民收入的提高而自动增加。

当然也存在着另一种假设，即在边际税率为正的情况下，如果(c+h)有时大于1，那么，财政支出的增加，不仅不会迫使税率提高，而且还会改善财政收支状况。这种情形对于财政当局来说当然是称心如意的，但在现实中，这种情况出现的概率很小。

最后，求得国民收入变化额对财政盈余变化额的比率。

用(10)式的两边分别去除(13)式的两边，得到：

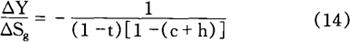
通过(14)式，可以理解赤字支出的乘数效应。式中的△Y和△S_g，是基于G′等内生变量的变化而产生的变化额。

因此，这与原来的乘数有所区别，资产阶级经济学家有时也称之为“虚拟乘数”。

财政支出政策效应图解 财政支出的变化对国民收入均衡值的影响，也可以利用图解法来说明。

在图1中，最初的均衡国民收入水平是由(C+I+G′)曲线和R₀R₀曲线相交点确定的OX₀。假定财政支出从G₀′提高到G₀′，于是，国民支出曲线就会向左上方移动，变成(C+I+G₀′)曲线。

新的均衡国民收入水平由这条曲线与R₀R₀曲线的交点决定，即OX₁。在图1中，△Y=X₀X₁，△G′=QE。

只要国民支出曲线的斜率(c+h)为正值，则△Y＞△G′。

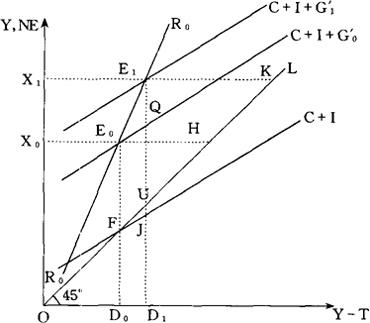
图1 财政支出水平的变动效应

这是在财政支出乘数大于1的情况下财政支出效应的图解。一般情况下，国民支出曲线的斜率增大直接影响到X₀X₁的大小，而国民收入曲线的斜率增大会有相反的效果。这表明，乘数值与(c+h)作相同方向变化，而与t值呈相反方向变化。

现在考察财政支出变化对财政状况的影响。在图1中，首先假定财政是平衡的。也就是说，T₀=E₀H=FE₀=G₀′。

新的税收收入是T₁，T₁=E₁K=UE₁，并且，G₁′=JE₁。

可见，财政支出增加QE₁，使得财政出现了赤字，即UJ=UE₁－JE₁。比较图中FJU与E₀QE₁这两个三角形的大小，就可知道财政收支的恶化程度(UJ)比财政支出的增加额(△G′=QE₁)要小。这是因为E₀Q与FJ平行，只要t＞0，E₀E₁的斜率就会比FU的斜率(=1)大。

3．税收乘数

在讨论财政支出乘数时，假定税率是既定的。现在相反，假定财政支出不变，分析税收政策的变化对国民收入水平的影响。

推导 税收乘数指因政府税收增加(减少)而引起的国民生产总值或国民收入减少(增加)的倍数。

在讨论税收政策时，主要是分析所得税。在这种税收政策中，被看成是计划变量的主要是各种扣除和超额累进税率。

在上述简单的模式中，与这种计划变量接近的是b和t。现假定财政支出G以及实际边际税率t不变，只有b从b₀变为b₁。这种操作表示在各种国民收入水平下使税收收入额发生△b(=b₁－b₀)的变化，即如此增税或减税。

由此引起的国民收入Y的变化额，可利用(9)式求得：

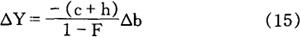
(15)式的经济意义在于：税收参数b增大的冲击效应(第一轮效应)，会使可支配收入同额减少，结果导致的最终需求的第一轮减少额等于－(c+h)△b。

现假定b不变，实际边际税率从t₀变为t₁。在这种情况下，如果最初的国民收入水平为Y₀，则最终需求的第一轮变化等于－(c+h)Y₀△t。

如果采用与新的实际边际税率相对应的支出乘数，就可得到Y的变化额。设(c+h)(1－t₁)=F₁，则：

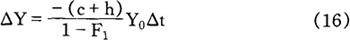
在(15)式和(16)式中，△b或Y₀△t表示在既定的国民收入水平下，税收冲击的变化额。如再乘上－(c+h)／(1－F)，就可得到国民收入变化额。资产阶级经济学家称之为“税收乘数”。

税收乘数与财政支出乘数相反，它是负值，表明增税或减税对国民收入的减少或增加效果。该乘数绝对值的大小，即税收政策影响Y的强度，与c和h的大小呈同方向变化，而与t的大小呈反方向变化。

于是，只要

c+h＞1－(c+h)(1－t)

或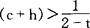

的条件存在，税收乘数的绝对值就大于1。

需要注意的几个问题 上述推导出来的税收乘数是在极其简单的模式中进行的。

前一节已经指出，价格水平变动的可能性、利率变化对投资的影响以及货币资产对消费的影响等都未予考虑。除此以外，还需要注意以下几点：

第一，这里所说的税收是指一般作为直接税的税收，特别是所得税；同时也不考虑税收转嫁问题。

至于间接税或税负可以转移的所得税，必须采用其他方法来分析。

第二，在国民收入水平既定情况下，增税或减税将直接使可支配收入发生减增变动，从而影响到民间消费，这是税收对消费的收入效应。

此外，增税使储蓄的税后收益率下降，这对消费也许能产生一定程度的影响。

第三，在可支配收入发生一定变化的情况下，民间支出的第一次变动额，取决于现在的变化对将来的可支配收入的预期值的影响。从这一点来看，如果税率的升高预期是暂时的，那么，税率的短期变动对民间支出的抑制效应低于长期变动。所以，政府在提出调整税收政策时，应当注意到这一点。

第四，假定纳税人的边际支出倾向与整个经济的平均边际支出倾向相等。另外，对于不同纳税人之间的边际支出倾向的差异，也没有考虑在内。

第五，这里没有考虑税收政策的变化对劳动欲望和经营努力的影响。

第六，所得税的变动对民间消费和民间投资的影响，本节分析得比较笼统。实际上，个人所得税和公司所得税对这二者的影响是极为不同的。

税收政策与财政状况 下面考察税收政策对财政收支状况的影响。

根据

S_g=b+tY－G′

可得：

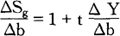
利用(15)式，将此式变形，则得到(17)式：

只要满足(c+h)＜1这个条件，该比率就可取比1小的正值。也就是说，b的提高会改善财政收支状况，但财政盈余的增加额要比△b小。

这是因为，在国民收入下降的情况下，存在着税收自动减少这样的抵消因素。这一因素的影响程度，越是在t高且(c+h)大时，就越大。

如果用税收乘数

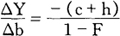
的两边去除(17)式的两边，可得到：

此式表明的是，税收政策的实施所引起的财政盈余的变化额与国民收入的变化额之间关系的虚拟乘数。与此对应的是前一节推导出的(14)式，只不过△Y／△S_g在这两式中所表明的经济意义不同。

所以，在(18)式中，左式加上了“*”号。比较两式的绝对值，可见在(c+h)＜1的条件下，(14)式一般较大。

这就说明，税收政策(如减税)导致的一定的财政赤字的增加，所产生的国民收入的增加额要比在支出政策情况下小。原因在于，首先，通过减税政策使可支配收入第一轮增加的部分，一般是用于增加个人储蓄，而不是用来增加最终消费需求。其次，政府支出同投资支出一样，引起的总支出变动包括自发支出变动和诱发支出变动，而且诱发支出变动一般远远大于自发支出变动。税收变动产生的直接影响是改变居民的可支配收入，从而改变消费支出。

税收引起的总支出变动仅包括诱发的消费支出变动。因此，财政支出乘数与税收乘数的关系用公式表示是：税收乘数=边际支出倾向×财政支出乘数，即

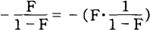
一般来说，边际支出倾向F的值小于1，因此，税收乘数小于财政支出乘数。根据上述分析，资产阶级经济学家认为，在现实的财政政策制定中，不能简单地强调赤字政策的一般乘数效应。

税收政策效应图解 税收政策对国民收入水平的影响，同支出政策一样，也能用图解方式加以说明。

图2中的R₀R₀表示在最初的税率表的情况下的国民收入曲线。最初的国民收入水平OX₀，是由国民支出曲线(C+I+G₀′)和国民收入曲线的相交点E₀决定的。这里，设定税收参数b从b₀上升到b₁。这样，由于税收政策参数变化(△b)而使国民收入曲线向左上方移动，变成R₁R₁。

Y的均衡值则下降到由R₁R₁曲线和国民支出曲线的交点E₁决定的OX₁。根据图示可知，国民收入的下降额△Y=X₀X₁；而且，国民收入曲线的斜率越小，而国民支出曲线的斜率越大，国民收入的下降额就越大。

在初始状态下，税收E₀H与财政支出FE₀相等，预算处于平衡状态。

当税率上升时，虽然税收增加E₁K，但财政支出水平没有变化，即FE₀=JE₁。在这种情况下，财政盈余产生了，即UJ=E₁K－JE₁=UE₁－JE₁。其数额要比△b(=BE₀)小。

这是由于在国民收入Y下降的情况下，导致税收减少。

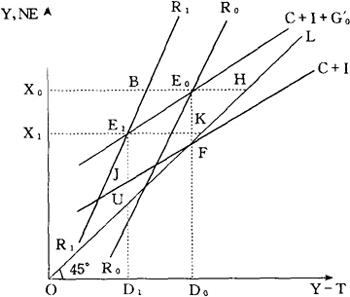
图2 税率变动的效应

4．平衡预算乘数

前两节说明的是，假定财政支出水平或税率两者中，有一个因素不变，而另一个因素发生变动的政策效应。

其实，这两者都能使财政收支的平衡状况发生变化。如果在政策上，要维持预算平衡，财政支出和税率就必须在一定的条件下互动。在这一约束条件下，政府变动预算规模之后，国民收入水平会受到怎样的影响呢?本节将考察这一问题。

平衡预算乘数指政府支出与税收同时且相等的变化而引起的国民生产总值或国民收入减少或增加的倍数。

该理论的核心是政府支出的扩张效应超出了税收的紧缩效应，其净效应是正数而不是凯恩斯以前经济学基本常识所说的零。换言之，用税收筹措的公共支出的增加将是扩张性的，而不是中性的。可以说，平衡预算乘数理论在经济学教科书中已成为一种无可辩驳的经济理论。当然，也有一些研究对平衡预算乘数理论提出质疑(Pullen，1982)。

平衡预算乘数理论的简史在“凯恩斯革命”爆发之前，经济学的常识是政府支出与税收同时且等量的变化对总需求变化的净效应为零；或者说，用税收融资的公共支出的增加是中性的，而不是扩张性的。但是，凯恩斯主义经济学诞生之后，经济学家们才把总需求可能受到财政措施的巨大影响概念化，平衡预算乘数理论才由格尔汀(Gelting，1941，p．36－42)、萨缪尔森(Samuelson，1943)、沃利克(Wallich，1944，p．78－91)以及汉森和波利夫(Hansen and Perloff，1943)等以各种形式传播开来，特别是沃利克的文章引起了对平衡预算乘数概念的热烈讨论。

1945年，哈维尔莫(Haavelmo，1945，p．311－318)进一步精炼了这一概念，并得到确切的结论：平衡预算变化具有直接的乘数效应，乘数值等于1。后来，图维(Turvey，1953，p．275－295)、鲍莫尔和佩斯顿(Baumol and Peston，1955，p．140－148)对该理论作了一般性概括，使该理论得到完善和定型。

平衡预算乘数理论与19世纪正统经济思想的主要组成部分——国库观(treasury views)形成了鲜明对照。

根据国库观，刺激经济不是政府的职责，政府这样做的任何企图，不仅是对私人个人权利的粗暴干涉，而且也是徒劳的。

财政部没有能力利用财政措施来刺激经济，因为，政府支出对经济的任何刺激效应，恰好被为支出融资的税收所产生的抑制效应所抵消。

可是，按照凯恩斯主义经济学原理，在经济萧条时期，政府要促进经济增长，要么采取赤字预算，要么采取把收入从低消费倾向阶层再分配给高消费倾向阶层的预算。

更有甚者，平衡预算乘数理论则认为，即使纳税人的平均消费倾向与政府支出受益人的平均消费倾向毫无二致，或者说，即使不存在高消费倾向阶层与低消费倾向阶层之间的收入转移，或者说，即使政府支出全部都有益于富有阶层，这种没有收入再分配的平衡预算也会产生刺激效应。因此，平衡预算乘数理论不仅涉及到抽象的理论问题，还存在着分配、福利和政治含义。

无论平衡预算乘数理论的奠基者的动机如何，事实依然是：通过减少预算赤字，削弱政府在经济中的作用——这只是“削弱”，而不是“消除”。平衡预算乘数理论借助平衡预算概念强化这种信念并赢得广泛支持，即政府通过最低限度的干预，就可以使经济增长和繁荣。

平衡预算乘数理论自20世纪40年代出现以来，得到迅速而广泛的接受，现已成为一种标准的经济学说。从某种意义上说，它甚至可与收益递减规律、比较优势等理论相媲美。然而，这一理论引发出许多令人思考的问题：它为何产生于20世纪40年代而不是19世纪40年代?导致这种理论出现的政治、经济环境是什么?其奠基者的动机是出于政治上的考虑还是收入再分配上的考虑?它是一种纯粹的经济理论的发展还是反映出有关个人与国家在经济事务中相对作用的特定思想?这些问题仍需要进一步探讨。

推导1 现在从预算保持一定规模的平衡状态出发，假定财政支出增加△G′。

为维持G′=T=b+tY这一条件的存在，假定税收参数b同时变动。

在考虑到国民收入变化的情况下，b的变化额必须满足下列条件：

△G′=△b+t△Y (19)

另一方面，根据决定均衡国民收入水平的(9)式，得到下列关系式：

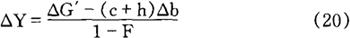
如果以△G′的值是已知的为前提条件，则(19)式和(20)式就可以看成是以△Y和△b为未知数的联立方程式。在(c+h)＜1的假定前提下，该联立方程的解为：

△Y=△G′ (21)

△b=(1－t)△G′ (22)

也就是说，为了维持预算平衡，在增加财政支出的同时，税收也要增加。由于国民收入正好只增加△G，而由此引起的税收的自然增加是t△G′，所以，△T=(1－t)△G′+t△G′=△G′，从而保持了预算平衡。

如同上述所分析的那样，如果用△B′来表示平衡预算规模的变化，将△Y／△B叫作“平衡预算乘数”的话，在上述简单的模型中，就是：

这就是说，一般情况下，国民收入水平变化等于平衡预算规模变化(△Y=△B′)，而与可支配收入决定的边际支出倾向的大小无关。原因在于，平衡预算规模的变动对总需求的冲击效应，由政府需求的变化(△G′)与民间需求的反方向变化－(c+h)△b=－(c+h)(1－t)△G′所构成。

因此，作为两者之和的总需求，其初始变化就是(1－F)△G′。这无非是政府支出的变化额与支出乘数的倒数之积。c+h的值增大，虽然减少了初始需求的变化，但是，它会提高支出乘数的值。由于这些作用正好相互抵消，平衡预算乘数就与c+h的值无关。

预算平衡乘数的经济意义在于，当经济处于萧条时期时，政府可以通过适当地增税来弥补等量的政府支出，这样既可以提高国民产出和就业水平，又可以避免财政赤字。

推导2 佩斯顿(佩斯顿，1992，第1卷，第191页)根据财政收支变化对国内总需求的影响，利用无限级数形式对平衡预算乘数进行了推导。政府在国内生产的产品和劳务的支出上增加一个单位，对总需求的影响由下列级数表示：

1+c+c²+…

所得税收入增加一个单位的影响由下列级数表示：

c+c²+…

注意，两个级数中的c都是指边际消费倾向。

如果以前一级数减去后一级数，所得到的1就是对总需求的净效应，即平衡预算乘数为1。

推导3 多巴氏和费雪(多巴氏和费雪，1982，第105页～第107页)根据总需求的变化量等于政府支出的变化量加上消费的变化量来推导平衡预算乘数。

假定消费的变化量等于来自可支配收入的边际消费倾向(c)乘上可支配收入的变化量(△Y_d)而可支配收入等于产量的变化量(△Y₀)减去税收的变化量(△T)。

于是：

△A=△G′+c(△Y₀－△T)

式中，△A代表总需求的变化量，△G′代表政府支出的变化量。一个均衡达到另一个均衡的过程中，总需求的变化量必然等于生产量的变化量。

所以，

△Y₀=△G′+c(△Y₀－△T) (24)

或者，

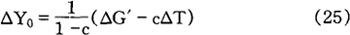
政府支出在新均衡与旧均衡之间的变化量正好等于税收的变化量，从而△G′=△T。把此式代入(25)式，在对财政政策的特定限制条件下，得到：

因此，平衡预算乘数正好等于1。

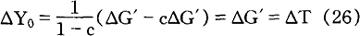
推导4 多巴氏和费雪(多巴氏和费雪，1982，第105页～第107页)还根据储蓄、税收、投资、财政支出所表示的商品市场的均衡条件来推导平衡预算乘数。

在国民收入决定理论中，

S+T=I+G (27)

同时，预算限制式可写成：

B=T－G

根据(27)式可知，

B=I－S (28)

如果预算与投资都不变化，储蓄的均衡变化就等于零。

由于储蓄没有变化，因而收入也必须保持不变，即

△Y_d=△Y－△T=0

从而再一次表示收入的变化量等于税收的变化量，而税收的变化量又等于财政支出的变化量。所以，由不变的预算盈余或预算赤字所诱发的乘数等于1。

这一证明过程说明了一个事实：一个部门的盈余或不足的变化将被另一个部门的不足或盈余的抵消。

如果财政盈余因受控于财政政策而保持不变，那么，私人部门的盈余(S－I)也必须保持不变。

需要注意的几个问题 第一，平衡预算乘数等于1这个命题，取决于为讨论方便而假定的许多条件。这些条件包括：(1)政府耗竭性支出用于取得本国经济新生产的物品；(2)社会的边际消费倾向和边际储蓄倾向在平衡预算乘数起作用期间不发生变化；(3)预算规模变化不改变对私人投资的刺激；(4)在整个经济中，无论是纳税人还是政府支出利益的受益人，边际消费倾向和边际储蓄倾向都相等；(5)工作－闲暇习惯不会因政府的预算措施而改变；(6)所涉及的税种与国民收入没有函数关系，亦即边际税收倾向(marginal propensity to tax，MPT)。

有的经济学家认为，如果在政府的商品和劳务支出中，有些是用来购买土地这种本期产品以外资产的，而且对卖方支出无直接影响，那么，平衡预算乘数为1－j(Baumol and Peston，1955，p．140－148；Holzman and Zellner，1958，p．73－91)。

第二，税收T的增加对消费C和投资I产生的影响，同对国民收入Y的影响相比，即使程度一样，但作用却有差异。在某些假设条件下｛这时的国民收入决定方程式为：

Y=C+I+jG′=a+cY－c′(b+tY)+e+hY－h′(b+tY)+jG′

所以，

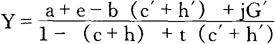
由此式可得：

［1－(c+h)+t(c′+h′)］△Y

=j△G′－(c′+h′)△b

把△b=△G′－t△Y代入此式，即可得到上列乘数式｝，平衡预算乘数变为下列形式：

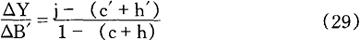
按照原来的假设，即0＜(c+h)＜1，所以，当j≥(c′+h′)时，△Y／△B≥0。乘数值正好等于1，只是j－(c′+h′)=1－(c+h)这一条件太特殊了。

第三，还有许多影响平衡预算乘数的因素没有讨论，所以，平衡预算定理的政策意义不应该体现在其乘数值等于1这一点上。传统理论认为，平衡预算规模的变化对国民收入的影响是中性的，而平衡预算乘数的政策意义就在于，它表明了这个传统观念是不正确的。

传统的看法是征税会等额地削减民间支出。用这里所说的模式来讲，无非是c+h=1。

在这种情况下，G′和b产生同样的变化，对总需求的冲击效应是△G′－(c+h)△b=0，故国民收入Y的均衡水平不变，平衡预算中性观点成立。但是，如果不是在这个极其特殊的条件下，传统观点就站不住脚了。

第四，平衡预算乘数概念仅与耗竭性支出有关，而不包含转移性支出。换言之，如果全部政府支出是转移性支出，那么，平衡预算变化可能是中性的，因为政府可能仅把购买力从纳税人转移到受益人。

也就是说，在这种情况下，政府做出直接的消耗资源的支出决策，所有支出决策仍然是由私人部门做出的。但是，“完全中性”可能需要下列严格假设条件，即纳税人与受益人之间的边际消费倾向和边际储蓄倾向完全相同。

平衡预算政策效应图解 利用图示对平衡预算的乘数效应加以进一步说明。

在图3，初始均衡点是(C+I+G′)曲线与R₀R₀曲线的交点E₀。税收E₀H和财政支出FE₀正好相等，此时，预算是平衡的。在这里，政府预算规模的变动只是提高支出水平，提高的幅度为E₀E₁，新的国民支出曲线为(C+I+G₁′)。

在这种情况下，为了维持预算的平衡，可以适当地变动税率表，以便使国民收入曲线在原均衡点E₀的正上方，并同新的国民支出曲线相交。图中表示的是只改变b所进行的调整。

新的均衡国民收入水平是均衡点E₁所对应的OX₁，新的税收收入额E₁K正好与G₁′(=FE₁)相等。并且，国民收入增加额△Y=X₀X₁与政府支出的增加额△G′(=E₀E₁)相等。可支配收入在OD₀水平上不变，故民间支出也和过去一样，只停留在D₀F水平上。

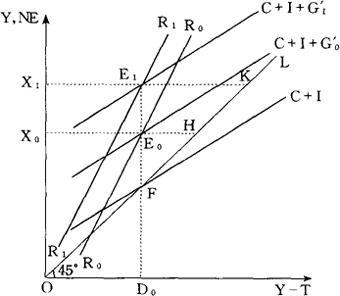
图3 平衡预算乘数效应

【参考文献】：

乘数理论(Multiplier Theory)

财政稳定器(Fiscal stabilizer)

Baumol, W. J. and M. H. Peston, 1955, More on the Multiplier Effects of a Balanced Budget, American Economic Review 45.

Gelting, J. H., 1941, Some Observations on the Financing of Public Activity, History of Polictical Economy 7 (1975).

Haavelmo, T., 1945, Multiplier Effects of a Balanced Budget, Econometrica, October.

Hansen, A. H. and H. S. Perloff, 1943, State and Local Finance in the National Economy, W. W. Norton & Co., Inc. .

Herber, B. P., 1971, Modern Public Finance: the Study of Public Sector Economics, Richard D. Irwin, Inc..

Holzman, F. D. and A. Zellner, 1958, Foreign Trade, Balanced Budget Multipliers, American Economic Review, March.

Kahn, R., 1931, The Relation of Home Investment to Unemployment, Economic Journal 41, June.

Pullen, J. M., 1982, The Balanced Budget Multiplier Theorem: Some Commets on its History, and A Critique, University of New England, Research Report or Occasional Paper No. 68.

Samuelson, P. A., 1943, Full Employment after the War, in; S. Harris, ed.. Postwar Economic Problems, McGraw-Hill Book Co. .

Turvey, R., 1953, Some Notes on Multiplier Theory, American Economic Review 43.

Wallich, W. W., 1944, Income Generating Effects of a Balanced Budget, Quarterly Journal of Economics, November.

多巴氏，R．和S．费雪，1982，《宏观经济学》，(台)1982年版。

佩斯顿，M．H．，1992，《平衡预算乘数》，载于约翰·伊特韦尔、默里·米尔盖特和彼得·纽曼主编，《新帕尔格雷夫经济学大辞典》，经济科学出版社中译版。

藤田晴，1966，《财政政策的理论》，(日)劲草书房。