数学的三次危机

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第897页（1266字）

指数学发展史中关于数学基础研究的三次危机。

第一次危机，大约发生在公元前5世纪。当时古希腊毕达哥拉斯学派发现，一个等腰直角三角形的直角边与斜边无公度；若三角形两直角边均等于1，则斜边长等于。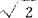

这一方面对当时人们关于“数”的认识只停留在有理数概念的初期阶段，特别是普遍认为一切量均可用有理数表示的情况下，是一个矛盾；另一方面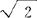，的出现，与毕达哥拉斯学派关于“数即万物”(这里的数指的是整数)的主张和信条，也发生了冲突。因此，上述发现，在当时被看成是“违反常识的”，是“荒谬的”；同时，由于它直接涉及到“数”这一数学最基本的概念，又使人们产生了关于数学基础的“危机感”。

这就是所谓数学的第一次危机。第二次危机，产生于17、18世纪，主要是由于微积分的出现而引起的。

17世纪下半叶，牛顿和莱布尼茨在前人研究成果基础上，大体上完成了微积分的创立工作，并且由于实践的需要微积分理论不断得到发展。然而，由于牛顿和莱布尼茨所建立的微积分，运用了含糊不清的无穷小概念，在推导函数时，毫无根据地去掉一些项，出现逻辑上的矛盾，造成了微积分的“神秘性”，因此遭到了来自各方面的特别是正统派数学家的激烈反对并引起争沦。

人们就把这次关于微积分基础理论方面的争沦以及由此所引起的数学界的混乱状况，称之为数学的第二次危机。经过一个多世纪的论战之后，于19世纪上半叶形成了数学界有名的“分析批判运动”，其主要代表人物是高斯(Gauss，C．F．)、柯西(Cauchy，A．L．)和阿贝尔(Appel，K．)等。

柯西建立了系统的极限理论，戴德金(Dedekind，R．)在实数论的基础上证明了极限论的基本定理，康托尔(Cantor，G．)和魏尔斯特拉斯(Weierstrass，K．)也在微积分基础研究方面做出了重要贡献。一般认为，由柯西极限概念建立起来的严格的微积分理论出现后，便结束了对微积分的非难，解决了数学的第二次危机。

马克思对牛顿和莱布尼茨建立起来的神秘微分学以及由此所引起的论争评论说：“于是，人们自己相信了新发现的算法的神秘性。……人们就这样把自己神秘化了，对这新发现评价更高了，使一群旧式正统派数学家更加恼怒，并且激起了敌对的叫嚣，这种叫嚣甚至在数学界以外产生了反响，而为新事物开拓道路，这是必然的。

”(《数学手稿》第88页)数学的第三次危机，出现在19世纪70年代康托尔创立“集合论”之后。由于建立严格的分析理论是以实数理论为基础的，而要建立严格的实数理论又必须以集合论为基础，集合论在数学基础研究中起着极为重要的作用。

但是，人们却发现了一系列关于集合论的悖论。其中罗素悖论最为突出，因为它不仅触及集合论中最基本的集合概念，而且还涉及到逻辑推理本身的问题，因而引起了广大数学家的震惊、不安和争论，并产生了新的关于数学基础的危机感。

围绕集合论悖论所展开的激烈争论过程中，形成了着名的关于数学基础研究的逻辑主义、直觉主义和形式主义等不同学派。人们就把集合论悖论的出现以及由此引起的争论称之为数学的第三次危机。