误差传播定律

出处：按学科分类—工业技术 中国建材工业出版社《工程测量实用技术手册》第96页（1622字）

当对某量进行了一系列的观测后，观测值的精度可用中误差来衡量。但在实际工作中，往往会遇到某些量的大小并不是直接测定的，而是由观测值通过一定的函数关系间接计算出来的。例如，水准测量中，在一测站上测得后、前视读数分别为a，b，则高差h=a－b，这时高差h就是直接观测值a，b的函数。当a，b存在误差时，h也受其影响而产生误差，这就是所谓的误差传播。阐述观测值中误差与观测值函数中误差之间关系的定律称为误差传播定律。

本节就以下四种常见的函数来讨论误差传播的情况。

1．倍数函数

设有函数

Z=kx

式中，k为常数，x为直接观测值，其中误差为m_x，现在求观测值函数Z的中误差m_Z。

设x和Z的真误差分别为△_x和△_Z，由上式知它们之间的关系为：

△_z=k△_x

若对x共观测了n次，则：

△_Zi=k△_xi (i=1，2，…，n)

将上式两端平方后相加，并除以n，得

按中误差定义可知，所以，上式可写成

或m_z=km_x即观测值倍数函数的中误差，等于观测值中误差乘倍数(常数)。

2．和差函数

设有函数

z=x±y

式中，x，y为独立观测值，它们的中误差分别为m_x和m_y，设真误差分别为△_x和△_y，由上式可得

△_z=△_x±△_y

若对x，y均观测了n次，则

△_zi=△_xi±△_yi (i=1，2，…，n)

将上式两端平方后相加，并除以n得

上式中[△_x△_y]的各项均为偶然误差。根据偶然误差的特性，当n越大时，式中最后一项将趋近于零，于是上式可写成

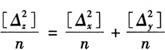
根据中误差定义，可得

即观测值和差函数的中误差平方，等于两观测值中误差的平方之和。

3．线性函数

设有线性函数

z=k₁x₁±k₂x₂±…±k_nx_n

式中，x₁，x₂，…，x_n为独立观测值，k₁，k₂，…，k_n为常数，则z的中误差为

4．一般函数

设有一般函数

z=f(x₁，x₂，…，x_n)

式中，x₁，x₂，…，x_n为独立观测值，已知其中误差为m_i(i=1，2，…，n)。

当x_i具有真误差△_i时，函数z则产生相应的真误差△_z，因为真误差△是一微小量，故将上式取全微分，将其化为线性函数，并以真误差符号“△”代替微分符号“d”，得

式中，是函数对x_i取的偏导数并用观测值代入算出的数值，它们是常数，因此，上式变成了线性函数，按式得

上式是误差传播定律的一般形式。前述的几个函数都可看作上式的特例。