数制变换

出处：按学科分类—工业技术 江苏科学技术出版社《简明电工计算手册》第31页（3670字）

1．常用计数制

(1)十进制数

十进制数由0～9十个不同的数码符号组成，并且逢“十”进位。任意一个十进制数A可表示为

A=a_n－1·10^n－1+a_n－2·10^n－2+…+a₁·10¹+a₀·10⁰+a_－1·10^－1+a_－2·10^－2+…

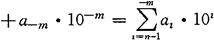
式中 A——任意一个十进制数；

i——数的某一位；

a_i——第i位的数码，即0～9中任一个数码；

n——数A整数部分的位数；

m——数A小数部分的位数；

10——十进制的基数。

［例1－1］ (2734．65)₁₀=2×10³+7×10²+3×10¹+4×10⁰+6×10^－1+5×10^－2

(2)二进制数

二进制数由0和1两个数码符号组成，并且逢“二”进位。其表达式为

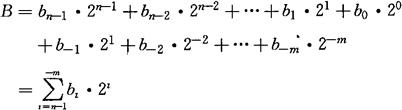
式中 B——任意一个二进制数；

i——数的某一位；

b_i——第i位的数码，即0或1；

n——数B整数部分的位数；

m——数B小数部分的位数；

2——二进制的基数。

［例1－2］ (1011．01)₂=1×2³+0×2²+1×2¹+1×2⁰+0×2^－1+1×2^－2

(3)八进制数

八进制数由0～7八个数码符号组成，并且逢“八”进位。其表达式为

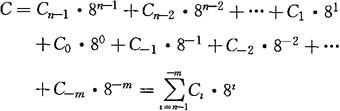
式中 C——任意一个八进制数；

i——数的某一位；

C_i——第i位的数码，即0～7中任一个数码；

n——数C整数部分的位数；

m——数C小数部分的位数；

8——八进制的基数。

［例1－3］ (163．25)₈=1×8²+6×8¹+3×8⁰+2×8^－1+5×8^－2

(4)十六进制数

十六进制数由0～9和A～F十六个数码符号组成，并且逢“十六”进位。其表达式为

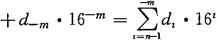
式中 D——任意一个十六进制数；

i——数的某一位；

d_i——第i位的数码，即0～9和A～F中任一数码；

n——数D整数部分的位数；

m——数D小数部分的位数；

16——十六进制的基数。

［例1－4］ (52A．1C)₁₆=5×16²+2×16¹+A×16⁰+1×16^-1+C×16^－2

上式中A相当于十进制数中的10，C相当于12。

2．常用计数制之间的转换

常用计数制数码对照见表1－22。

表1－22 十进制、二进制、八进制、十六进制数码对照表

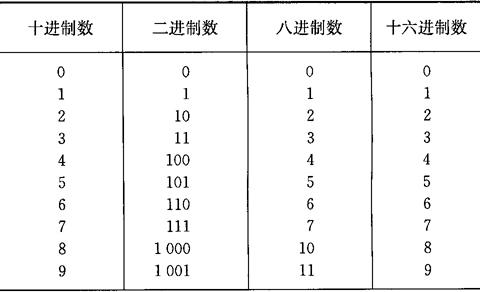
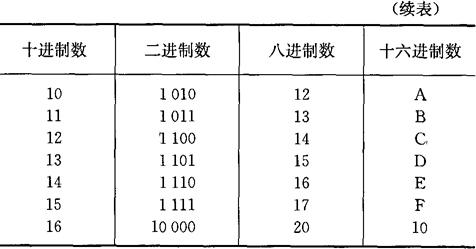
(1)二进制、八进制、十六进制数与十进制数之间的转换

二进制、八进制、十六进制数转换成十进制数的方法为

式中 K——某一任意进制数；

i——数的某一位；

k_i——第i位的数码；

n——数K整数部分的位数；

m—－数K小数部分的位数；

x——任意进制的基数。

［例1－5］ (1101．101)₂=1×2³+1×2²+1×2⁰+1×2^－1+1×2^－3=(13．625)₁₀

［例1－6］ (263．74)₈=2×8²+6×8¹+3×8⁰+7×8^－1+4×8^－2=(179．9375)₁₀

［例1－7］ (5A2．C8)₁₆=5×16²+10×16¹+2×16⁰+12×16^－1+8×16^－2=(1442．78125)₁₀

十进制数转换成二进制数的方法是整数部分除2取余数，小数部分乘2取整数。

［例1－8］ 把十进制数109．8125转换成二进制数。

［解］ 整数部分转换方法为：

因此，(109)₁₀=(1101101)₂

小数部分转换方法为：

因此，(0．8125)₁₀=(0．1101)₂

所以，(109．8125)₁₀=(1101101．1101)₂

同样，十进制数转换成八进制数的方法是整数部分除8取余数和小数部分乘8取整数；十进制数转换成十六进制数的方法是整数部分除16取余数和小数部分乘16取整数。另外，也可先将十进制数转换成二进制数，再由二进制数转换成八进制或十六进制数。

(2)八进制数与二进制数之间的转换

每三位二进制数可用一位八进制数来表示，并且按表1－22中的对应关系来转换。

［例1－9］ (276．134)₈=(010111110．001011100)₂=(10111110．0010111)₂

［例1－10］ (1011101．00111)₂=(001011101．001110)₂=(135．16)₈

(3)十六进制数与二进制数之间的转换

每四位二进制数可用一位十六进制数来表示，并且按表1－22中的对应关系来转换。

［例1－11］ (5A4．6DC)₁₆=(010110100100．011011011100)₂=(10110100100．0110110111)₂

［例1－12］ (1101011011．01001111111)₂=(001101011011．010011111110)₂=(35B．4FE)₁₆