绞碎与斩拌的机理
出处：按学科分类—农业科学 中国轻工业出版社《肉类工业手册》第210页（10036字）
(一)固体颗粒组成及块度
1．颗粒组成与粒度
固体物料的颗粒组成是指物料按不同尺寸颗粒所占重量的百分比的分布情况。各种自然堆积的块状、颗粒和粉末状的物料，即散料，是由各种不同粒度的颗粒组成的。
颗粒的大小称为粒度，是表示固体碎裂程度的代表性尺寸。对于球形颗粒，其粒度即为直径。对于非球形颗粒，则有以面积、体积(或质量)为基准的粒度的各种表示法。
以表面积为基准的颗粒粒度是面积等于该颗粒表面积的球体直径。设颗粒的表面积为Sp，则以表面积为基准的粒度ds为：
以颗粒体积为基准的颗粒粒度是体积等于该颗粒体积的球体的直径。设颗粒的体积为Vp，则以体积为基准的粒度dv为：
颗粒粒度dv是工业上常用的颗粒代表尺寸，常称为颗粒的相当直径，多用符号dp表示。对于不规则但近似球形的颗粒，通过筛析可以求得近似的dv。但如颗粒远非球形，则筛析求得之值将偏大。对于规则而非球形的颗粒，筛析结果将根据颗粒形状而异。
由于绞碎(粉碎)机理的复杂性，固体破碎后的颗粒形状并非球形，而且变化很大。为了表示颗粒形状偏离球形的程度，常用球形度φs这一概念，其定义如下：
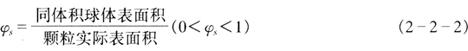
根据ds和dv的意义，显然可知：
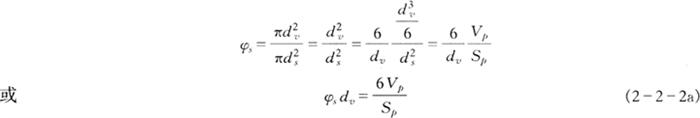
该公式表明球形度与颗粒的比表面积(Sp／Vp)有关。φs愈小，则比表面积愈大。对于许多碎裂物料，颗粒球形度常在0．6～0．7之间。对于球形颗粒，φs=1。对于立方体形颗粒，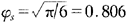
。
立方形和球形一样，都是规则的形状。为了表示颗粒形状偏离这些规则形状的程度，也有采用形状系数的概念。
设任意选取颗粒的某一代表性尺寸L，则必有：
Vp=aL3 Sp=6bL2 (2－2－2b)
这里，a和b是与颗粒的几何形状及代表性尺寸选择有关的系数。对于立方体，如选择边长为代表性尺寸，则a=b=1。对于球体，如选择直径为代表性尺寸，则a=b=π／6。
将上两式相除可得：
Ψ是颗粒根据代表性尺寸L的形状系数。可见形状系数不仅与表面积有关，而且与代表性尺寸的选择有关。如果按通常情况选取L=dv，则形状系数Ψ为球形度Ψs之倒数，对球体，Ψ等于1，对其它形状Ψ＞1。
2．块度与粒度分布
物料颗粒一般具有几个方向的线尺寸，块度则是指颗粒的最大线尺寸。根据固体颗粒粒度的典型尺寸，通常把散料分为：
大块物料 ＞160mm
中块物料 =60～160mm
小块物料 =10～60mm
小颗粒物料 =0．5～10mm
粉末状物料 ＜0．5mm
食品加工中常见的物料是小颗粒物料和粉末状物料。
固体颗粒碎裂后，不仅形状不一致，大小也不一致。全部颗粒中，粒度小于d的所有颗粒的粒数、表面积、体积(或质量)占全部颗粒的粒数、表面积、体积(或质量)的百分率，分别称为粒数、表面积、体积的累积分布函数，以符号AN(d)表示。粒数的累积分布AN(d)见图2－2－1。
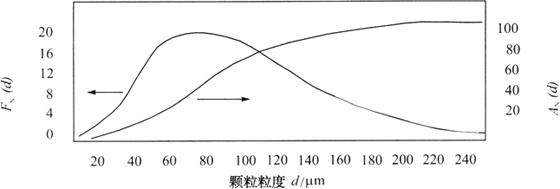
图2－2－1 颗粒粒数的频率分布和累积分布
颗粒分布有各种不同的测定方法，如显微分析法、筛析法和光吸收法等。测定结果找出各种粒度下的累积数，画出累积分布曲线。通常根据显微分析法所得的为粒数分布，筛析法所得的为体积(或质量)分布，光吸收法所得的为表面积分布。
如将累积分布函数对粒度d微分，即得频率分布函数f(d)。即：
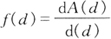
频率分布函数也有粒数(fN)、表面积(fs)和体积(fv)三种，其意义是：粒度为d、粒度增量为1单位范围内颗粒数目、表面积、体积所占的百分率。粒数分布曲线也画在图2－2－1上。由以上定义可知，若最小粒度为dmin、最大粒度为dmax，则有：
3．平均粒度
平均粒度有各种表示法，多数是以粒数的频率分布来进行加权平均。由于平均时所采用的基准和方法不同，所以有多种名称。所用的基准有粒度、表面积和体积三种，而所用方法则有算术平均、几何平均和调和平均等数种。
算术平均粒度dAM适用于过大和过细颗粒的并不太多，分布较为均衡时，几何平均粒度dGM对于对数正态分布来说是频率最大的粒度。调和平均粒度dHM则与颗粒的比表面积有关，所以当比表面积是制品的一项重要特征时，它是一种有意义的粒度。一般来说这三种粒度有如下的大小顺序，即dAM＞dGM＞dHM。
以上三种平均粒度都是直接按粒度本身来平均的。如果先用算术平均的方法求取颗粒的平均表面积，以后按此表面积来计算粒度，即为面积平均粒度(dsM)。所以面积平均粒度是反映颗粒平均表面积的一种粒度。另外还有体积平均粒度(dVM)，它是反映颗粒平均体积(或质量)的一种粒度。
调和平均粒度是反映颗粒比表面积的平均值的粒度。另外，如果以颗粒总体的平均表面积和平均体积为依据，则所得的粒度又从另一方面反映了颗粒比表面积，即体面平均粒度或沙得(Sauter)平均粒度，其定义为：
沙得平均粒度在食品的粒度分析上有广泛的应用。
(二)碎裂方法与碎裂力
固体物料的碎裂，可按被碎裂物料和成品的粒度大小，作如下分类：
(1)粗碎 原料粒度范围为40～1500mm，成品粒度为5～50mm；
(2)中、细碎 原料粒度范围为5～50mm，成品粒度为0．1～5mm；
(3)磨碎或研碎 原料粒度为2～5mm，成品粒度为0．1mm左右；
(4)胶体磨 原料粒度远小于磨碎的范围，而成品减少到0．01mm。由于胶体磨多为湿法操作，具有混合和超微碎裂以及乳化的作用，故放在第三节讨论。
在物料的绞碎(粉碎)操作中，常用“绞碎(粉碎)比”来表明物料碎裂前后粒度的变化程度。因此，物料绞碎(粉碎)前后的粒度比称为绞碎(粉碎)比或绞碎(粉碎)度。如以X表示，则
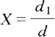
可见绞碎(粉碎)比表示绞碎(粉碎)操作中物料粒度变小的比例。磨碎时绞碎(粉碎)比较粗碎和中、细碎时为大。对一次绞碎(粉碎)后的绞碎(粉碎)比，粗碎为2～6，中、细碎为5～50，磨碎为50以上。总绞碎(粉碎)比是表示经过几道绞碎(粉碎)步骤后的总结果。
对于将大块固体物料绞碎(粉碎)为细粉的碎裂操作，由于一次绞碎(粉碎)比很大，常将其分为若干级，每级负担一定的绞碎(粉碎)比。典型的三级绞碎(粉碎)流程见图2－2－2。
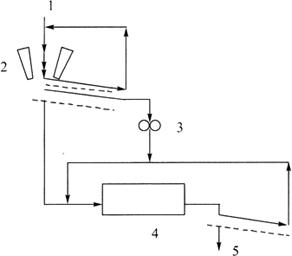
图2－2－2 典型绞碎(粉碎)流程
1－粗料 2－粗绞(颚式压碎机) 3－中、细碎(滚筒压碎机) 4－研磨(球磨机) 5－细粉制品
通常绞碎(粉碎)操作有好几种方法。每种方法有其特定的适用场合。这些方法包括开路磨碎、自由压碎、滞塞进料和闭路磨碎等。
开路磨碎是研磨设备操作的一种最简单的方法。这种办法不用振动筛等附属分粒设备，故设备投资费用低。物料加入绞碎(粉碎)机中经过绞碎(粉碎)作用区后，即作为制品卸出，粗粒不作再循环。由于有的粗粒很快通过绞碎(粉碎)机，而有的细粒在机内停留时间很长，故制品粒度分布很宽，能量利用不充分。
自由压碎操作法可以保持物料在作用区的停留时间很短。当与开路磨碎结合时，让物料借重力落入作用区，限制了细粒不必要的绞碎(粉碎)，因而减少了过细的粉末形成。此法在动力消耗方面较经济，但由于有些大颗粒迅速通过作用区，故可能产生较宽的粒度分布。
滞塞进料是利用机器出口插入筛网，以限制制品的卸出。对于给定的进料速率，制品滞塞于作用区，直至绞碎(粉碎)成能通过筛孔的大小时为止。因为停留时间可能长，故细粒受到过度绞碎(粉碎)，且功率消耗大。滞塞进料法常用于需要细碎制品的场合，以一台机器操作可获得很大的碎裂比。
闭路磨碎是从绞碎(粉碎)机出来的物料流先经分粒系统，分出过粗的料粒后，再重新回入绞碎(粉碎)机。在这种情况下，绞碎(粉碎)机的工作只是针对较大的颗粒，物料的停留时间短，所以动力消耗可以降低。所采用的分粒方法由送料的形式而定。采用重力法加料或机械螺旋送料时，常用振动筛作为分粒设备。当用水力或气力输送时，则常用旋风分离器。
绞碎(粉碎)操作除了上述所谓干法外，还有湿法。但被处理的原料为湿料或被湿润后无害的干料，则考虑采用此法。此时原料是悬浮于载体液流(常用水)中进行磨碎。此法可克服粉尘问题，并可采用淘析、沉降、离心分离等水力分级的方法来分离所需的制品。在食品加工中，磨碎经常作为浸出的预备操作，使组分易于溶出，故颇适于湿法绞碎(粉碎)法。
实践证明，湿法操作一般消耗能量较干法为大，同时设备的磨损也较严重。但湿法比干法易获得更细的制品，故此法在超细磨碎中应用甚为广泛。
物料绞碎(粉碎)时所受到的作用力主要有三种，即挤压力、冲击力和剪切力(或摩擦力)。其它如弯曲、扭转等则为附带的作用力。各种绞碎(粉碎)设备所产生的碎裂力不是单纯一种力，而是几种力的组合。但对特定的设备，则可以是以一种力为主要的碎裂力。
挤压力常用于坚硬物料的粗碎，冲击力可作为一般用途的碎裂力而用于食品物料的粗碎、中碎、细碎和磨碎，剪切力或摩擦力则被广泛应用于较软而无磨蚀性物料的磨碎。
绞肉机或斩拌机在绞肉或斩拌肉的过程中，主要是利用挤压力与剪切力的作用。斩拌机除了切刀的剪切力作用外，还有刀片的轴向旋转与料盘水平转动间的相对运动所起到的混合与乳化作用。
肉类在绞碎或搅拌操作中，在受到挤压力作用时，先是横向纤维变形。接着肉纤维被拉长，在挤压方向上变形减少，横向纤维和纵向纤维趋于一致。当变形达到极大值时，肌肉纤维就会发生瞬间断裂。经试验，牛肉在正常情况下，断裂强度p断=135～290kPa。其断裂强度随温度降低而增加，如羊肉在0℃以上，p断=205kPa，而在－10℃时，p断=980kPa。猪脊背肉与腰肉在－10℃时，p断=720kPa。
剪切力是肉在切割机械中刀具对肉所施加的切割力。据研究，对于硬的或半硬的猪肉，平均剪切应力为230kPa(－4～4℃)，且随温度降低而增加。因此，一般肉品加工中建议加工温度以－2～2℃为宜。另外，肉的剪切应力还与盐溶液浓度有关。当浓度为3%～5%时，剪切应力下降，在5%～8%时降低至最低。当浓度小于5%或大于15%，肌肉的剪切应力反而增加。
(三)绞碎(粉碎)的能耗和绞碎(粉碎)速率
1．绞碎(粉碎)的能量消耗
采用各种不同方法对物料进行绞碎的作用力主要为挤压力、剪切力和冲击力，另外还有弯曲、扭转等附带的作用力。在实际绞碎(粉碎)操作中，作用力是由上述几种力共同作用的结果。这些作用力由绞碎(粉碎)机械的一定部件传与物料之后，物料首先产生各种应变，并以各种形式的变形内能积蓄于物料内部。当局部积蓄的变形能超过某临界值时(其值取决于物料的性质)，碎裂就发生在脆弱的断裂线上。所以，从这一角度来分析，绞碎(粉碎)需要两方面的能量：一是碎裂发生前的变形能(即使未发生裂解，也终将转变为热)，这部分能量与颗粒的体积有关；二是碎裂发生后出现新表面所需的表面能，这部分能量与新出现的表面积的大小有关。当然还有颗粒间摩擦所消耗的能量。
到达临界状态(未裂解)的变形能之所以与颗粒的体积有关，是因为脆弱的断裂线和疵点对于粒度愈大的颗粒，存在的可能性就愈大。这样大颗粒所需的临界应力就较小颗粒为小，因而消耗的变形能也就较少。这就是绞碎(粉碎)操作为什么随着粒度减小而碎裂愈加困难的原因所在。
在颗粒粒度相同的情况下，由于物料的力学性质不同，所需的临界变形能也不相同。一般物料受应力作用时，在弹性极限应力以下，物料经受了弹性变形。当作用的应力在弹性极限应力以上，物料就经受永久变形，直至应力达到屈服应力。在屈服应力以上，物料开始流动，经历塑变区域，直至达到破坏应力而断裂。根据物料应变与应力的关系以及极限应力的不同，通常将物料的力学性质分成以下三种：①硬度：是根据物料的弹性模数的大小来划分的性质，即硬和软之分。②强度：是根据物料的弹性极限应力的大小来划分的性质，即强和弱之分。③脆度：是根据物料塑变区域的长短来划分，即脆性和可塑性之分。这样，对一种具体物料来说，就有比较复杂的性质，例如硬而脆的，软而脆的等等。这些性质对绞碎(粉碎)时所需的变形能均有影响。总的来说，凡是强度愈强、硬度愈小、脆性愈小的物料，所需的变形能愈多。必须指出，物料还有一项重要特性，称为韧性。韧性是一种抵抗物料裂缝扩展的能力的特性，韧性愈大，裂缝末端的应力集中愈易解除。
绞碎(粉碎)中出现新表面所需的能量与表面积的增量成正比，可表示为：
Eσ=△(σ·S)
式中 σ——物体表面的界面张力
S——表面积
2．绞碎(粉碎)的能耗法则
实践证明，绞碎(粉碎)操作中，因增加新的表面积而消耗的能量只占全部能耗的很小比例。但是计算绞碎(粉碎)操作所需的最低能耗是不容易的，理论上也很不成熟。早期的理论研究是建立在以下的假设之上，即固体颗粒的粒度d发生微小变化——d(d)时所需的能量dE是粒度的函数，作为一般式有如下形式：
此式当n=2时，经积分，则得：
此式早在1867年由雷廷格(Rittinger)提出，称为雷廷格法则。它是建立在表面积假说之上的能耗法则。设一粒度为d1的颗粒，当绞碎(粉碎)成n颗粒度为d2的小颗粒时，原颗粒的表面积
，n颗小颗粒的总表面积为
。因绞碎(粉碎)前后总体积不变，即
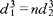，故有：
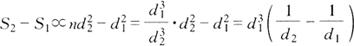
可见雷廷格式中的E∝S2－S1，即绞碎(粉碎)所需的能量与因绞碎(粉碎)而增加的新表面积成正比。所以此法适用于脆性物料、坚硬物料和大块物料的绞碎(粉碎)。
当n=1时，式(2－2－4)积分后所得：
此式即为1885年提出的基克(Kick)法则。基克法则是建立在体积学说之上。由于颗粒体积Vn∝d3，故dVn∝3d2d(d)，代入式(2－2－4)，令n=1，即有dE∝dVp／Vp，表示能耗与体积相对改变成正比。所以基克法则的能耗主要是变形能的消耗。故此式适用于塑性物料、软性物料和细粒物料的绞碎(粉碎)。
当式(2－2－4)中n=1．5时，所得为如下的朋特(Bond)法则(1952)：
朋特式的理论依据是介于表面积假设和体积假设之间。根据式(2－2－2a)显然可知：
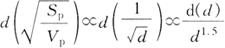
故朋特式实为绞碎(粉碎)能耗正比于颗粒表面积与体积之比的平方根的变化。
在实际应用上，雷廷格式和基克式不仅其计算结果可能相差很大，而且常与实际不相符合。所以在实际中常将式(2－2－5)直接积分后，由实验方法求取n，以此进行估算，积分式为：
所有上述各种能量式中，1／CR、1／CK、1／CB以及(n－1)／CL等均称为绞碎(粉碎)效率系数。
3．绞碎(粉碎)速率
设Rd为粒度大于d的物料体积(或质量)的百分率，根据1971年贝屈拉(Batra)和皮士瓦斯(Biswas)的建议，绞碎(粉碎)速率(－dRd／dt)可用如下的关系式来表达：
这里，k是一个只与粒度有关的系数，而m则为常数。
假设绞碎(粉碎)开始时的Rd为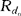
，通过上式积分即得下式：
如果通过实验，事先求出k、m，则可利用此式计算绞碎(粉碎)进行到一定的Rd时的绞碎(粉碎)时间t，或经一定绞碎(粉碎)时间t后所达到的Rd。
4．绞肉机的生产能力与能耗
绞肉机的生产能力主要由切刀的切割能力来决定，切刀的剪切力可用下式计算：
式中 F——切刀剪切力，cm2／h
n——切刀转速，r／min
D——格板直径，cm
φ——孔眼总面积与格板面积之比值(平均为0．3～0．4)
z——切刀总数(十字刀为4)
求出F后，可求出绞肉机的生产能力Q：
式中 Q——生产能力，kg／h
F——切刀剪切力，cm2／h
A——被切割1kg物料的面积，cm2／kg
a——切刀剪切力的利用系数(0．70～0．75)
关于F1的值，取决于物料的种类和格板上孔眼直径的大小。对于肉类，F1的值如下：
当孔径为2mm时，F1=11000～12000cm2／kg
当孔径为3mm时，F1=6000～7000cm2／kg
当孔径为25mm时，F1=700～1000cm2／kg
由此可见，孔径愈大，同样切割1kg物料的切割面积愈小，即F1愈小，则G愈大。所以粗绞生产能力比细绞大。
绞肉机的功率消耗，主要用于切割物料时的阻力。因此，知道切割1kg的能量消耗比率后，就可求得所需功率P：
式中 P——功率，kW
q——能量消耗比率，kW·h／kg
Q——生产能力，kg／h
η——传动效率
对于新鲜肉：
当孔眼直径为2mm时，能量消耗比率为0．004～0．005kW·h／kg
当孔眼直径为3mm时，能量消耗比率为0．0025～0．0030kW·h／kg
当孔眼直径为25mm时，能量消耗比率为0．0004kW·h／kg
对于冻肉：
当孔眼直径为2mm时，能量消耗比率为0．019kW·h／kg
当孔眼直径为3mm时，能量消耗比率为0．010kW·h／kg
5．斩拌机的生产能力与能耗
对于间隙操作的机器，生产能力由其规格尺寸、加工时间确定：
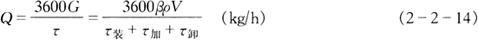
式中 G——肉料一次装入量，kg
β——料盘装满度，0．6，不大于0．8
ρ——肉料密度，kg／m3
V——料盘容积，L
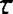——生产过程所延续时间，s。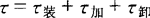
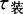——装料时间，s
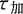——加工时间，s
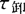——卸料时间，s
按单位能量消耗计算，可求得所需功率P：
P=qQ (kW) (2－2－15)
式中 q——单位消耗能量，kW·h／kg。加工肉块时，q=11～16；加工肉糜时，q=8～11
Q——生产能力，kg／h