用回归分析法预测基建钢材用量

出处：按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第1092页（2277字）

某公司是一个专门为输变电工程施工的企业。多年来，由于设计赶不上施工的需要，工程的建设不能按施工程序进行，工程所需的钢材计划，往往在没有纸和资料的情况下，凭经验估计编制。由于估计不准确，在不同程度上影响了加工及施工的进行。如何编制一个比较准确的备料计划呢?该公司根据多年在实践中积累的统计资料，试用回归分析法对钢材用量进行估计和预测。

一、预报年耗用钢材量回归直线方程的推导

1．该公司历年来耗用钢材量和完成工作量的情况(见表1)

表1 1974－1982年耗用钢材量与完成工作量表

为了分析钢材耗用量与完成工作之间的关系，设完成工作量为自变量，以x表示，耗用钢材量为因变量，用y表示，作成相关图(见图1)。

图1

由图1可以明显地看出，数据点近似直线变化。因此，可以用归直线来表示他们之间的关系Y=a+bx。

2．求=a+bx回归直线方程

根据表1数据，列出一元回归计算表(见表2)

表2

一元回来计算

表

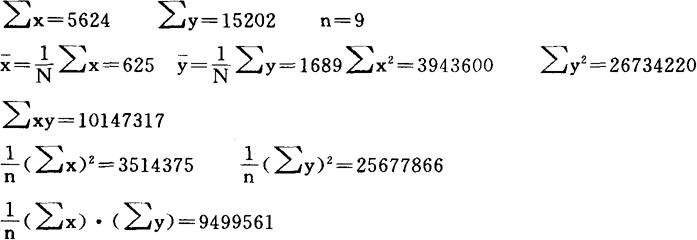
根据表2，可求解回归方程的系数如下。计算公式为：

将a、b系数值代入方程，即得到预测钢材用量及完成工作量之间的回归方程为：

=745+1．51x

表31980－1982年各类规格钢材消耗情况及1983年消耗预测值

注：本表钢材消耗量均四舍五入取整数。

将回归直线绘于图1。

从配制的回归线可以明显看出，随着完成工作量的增加，耗用钢材量也随之而增加，它们之间存在着正相关关系。这和实际情况是相符的。

二、试用回归直线方程=745+1．51x预测该公司1983年的钢材耗用量及准确性的检验

1．1983年这个公司钢材消耗总量的预测

上面对该公司九年来完成工作量与耗用钢材之间的关系进行了回归分析。回归分析的目的在于找出变量之间的变化规律，利用找到的规律，根据某些变量的已积压值，预测或控制另一些变量的值。他们试用上面推导的回归直线方程预测公司1983年钢材需用量。年初上级下达公司1983年工作量任务是1，150万元，将此值代入回归方程得：

=745+1．51×1，150=2，482(吨)，这就是这公司1983年钢材需用量的预测值。

2．各种规格钢材年消耗量的预测

对编制工程施工用料计划来讲，只知道总数是不够的，必edm知道具体规格的分量。为了预测分量的数值，下面统计了1980到1982年各种规格钢材的年消耗量。由于钢材规格很多，有常用的，也有极少使用的，同时根据过去在加工中规格接近的钢材常有相互代用的情况，把资料进行分类统计(见表3)。从表3可以看到各类规格钢材，各年消耗量有的相差无几，有的则差别很大。他们用简单的算术平均法把差异抽象化，以求出它们的平均消耗量和各占年耗总量的百分比，作为各类规格钢材用量的预测依据。

上面已预测出1983年钢材消耗总数为2，482吨。按上述百分比，便可计算出1983年各类规格的钢材的消耗量。计算结果列于表3中，这最后一项就是要1983年各类钢材消耗量的预测值，可作为年度工程使用钢材的备料计划数。

3．预测准确性的检验

1983年全公司共完成1147万元的工作量。按上面推导出的回归直线方程计算应消耗钢材

=745+1．51x=745+1．51×1，147=2，477(吨)。

1983年公司全年实际消耗钢材2，655吨，比用回归直线方程预测多178吨，准确程度达93．3%。

随着工程任务的变化和技术的更新，工作量和钢材消耗量之间的关系不可能是一成不变的，因此，要注意逐年积累资料，提高预测的准确程度。