用回归直线分析法预测收音机生产量

出处：按学科分类—经济 企业管理出版社《现代企业内部会计实用手册》第1106页（1801字）

某电子厂1980年用回归直线分析法预测1981年的的收音机生产量，为安排下年度的生产计划提供了科学依据。

一、收集数据

先将以往积累的资料，以年份为横坐X，每年销售量为纵坐标Y，列成下表(见表1)：

表1

将上表中数字点在一直角坐标系上，可以看出，这些点大致接近于一条直线(见图1)。

图1

二、作回归直线

回归直线必须在直角坐标系描点分布的中间，并尽可能使回归直线两边的描点数相等。从图1上可见此直线两边的描点数正好各为三点。因此可以用回归方程Y=a+bX来表示年份X与销售量Y之间的函数关系，某中a为回归方程中的常数，b为回归系数。根据此回归直，可近似预测出1981年(X=7)的销售量(Y)为22．1万架。也就是说，1981年的生产计划可安排22．1万架左右。

但是，由于直接利用图1上的回归直线来预测的误差较大，因此，再结合用最小平方法来求出误差最小的回归直线方程，以提高预测的精度。

三、用最小平方法求回归直线方程

最小平方法使倾向性的回归直线到实际各点之间的距离最小。说明这条回归线最能代表实际资料的发展趋势，因而也最适宜作为预测标准。

设：回归直线方程Y：=a+bti

列出表2，并求b、a。

根据公式

Y_i=a+bt_i=10．55+1．35t_i

根据回归方程Y_i=10．55+1．35预测1981年该厂收音机生产计划水平。

∵ 1980年的t_i=5，∴ 1981年的t_i=7；

∴ y_t=10．55+1．35×7=20(万)。

四、计算预测数与实际数值间的标准方差(σ)

根据公式：

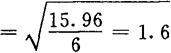
再计算1981年计划预测数在实现概率95．5%的数值。根据正态分布规律，实现概率95．5%时，其控制范围在Y_t±2σ之内。

因此，1981年收音机生产量预测数的分布上限和下限分别为：

上限 Y_t+2σ=20+2×1．6=23．2万

下限 Y_t+2σ=20+2×1．6=16．8万

作回归直线的上限、下限控制图(见图2)：

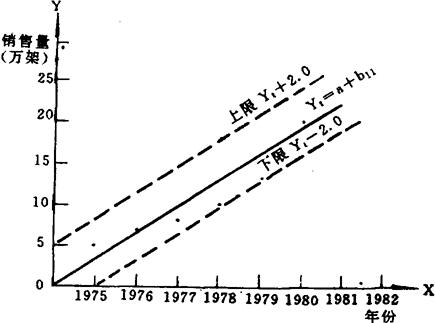
图2

五、结论

该厂1981年收音机生产计划水平通过回归直线法预测是近似22．1万架，并用最小平方法预测，实现概率在95．5%时，1981年生产计划水平在16．8万架～23．2万架之间。这两种预测方法结合起来分析，所预测的数字基本是一致的。根据该厂的生产能力和其他方面的原因，最后，初步确定1981年的收音机生产量为23万架。