常用曲线的极坐标方程及参数方程

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第15页（1077字）

圆的方程

r=R (圆心在极点，半径为R)；

r=2Rcosθ (圆心在x轴上且与的直线相切)；

r=2Rsinθ (圆心在y轴上且与极轴相切)．

双扭线方程及其图形(见图1．11)

图1．11

在直角坐标系中：(x²+y²)²－2a²(x²－y²)=0；

在极坐标系中：r²=2a²cos2θ．

摆线(或称普通旋轮线)方程及其图形

摆线的定义 定圆上－点M在直线上作不滑动的滚动的轨迹(见图1．12)．

图1．12

摆线的参数方程：(定点M开始时在坐标原点．)

星形线(或称m=4时的内摆线)的方程及其图形

星形线的定义 星形线是－圆周(直径为a)沿另－定圆(直径为4a即m=4)的内部不滑动而滚动时，圆周上－定点M所构成的轨迹(见图1．13)．

图1．13

星形线的方程：或(定点M开始时在x轴上．)

玫瑰线

1．心形线(见图1．14)

图1．14

2．三叶玫瑰线(见图1．15)

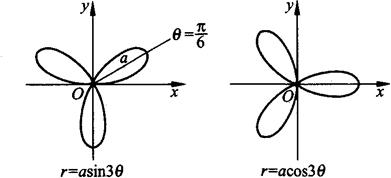
图1．15

3．蔓叶线(见图1．16)：y²(2a－x)=x³．

图1．16

4．笛卡儿叶形线(见图1．17)：x³+y³－3axy=0．

图1．17