导数

出处：按学科分类—数理科学和化学 清华大学出版社《数学手册（大学生用）》第46页（3537字）

导数的定义 设函数y=f(x)在点x₀的某邻域内有定义，当自变量x在x₀处取得增量△x时，相应的函数增量为

△y=f(x₀+△x)－f(x₀)．

如果

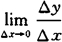
存在，则称函数y=f(x)在点x₀处可导，并称这个极限为函数y=f(x)在点x₀处的导数，记为

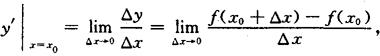
也可记作

导数的几何意义 f′(x₀)表示曲线y=f(x)在点M(x₀，f(x₀))处切线的斜率，即

f′(x₀)=tanα (α为倾角)(见图3．1)．

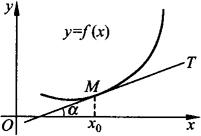
图3．1

切线公式 y－y₀=f′(x₀)(x－x₀)．

法线公式

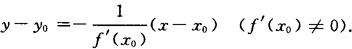
当f′(x₀)=0时，法线方程为x=x₀．

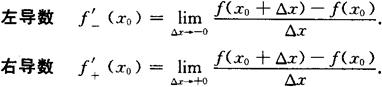
定理 函数f(x)在点x₀处可导左导数f′(x₀)和右导数f′+(x₀)都存在且相等．

开区间(a，b)内可导 如果函数y=f(x)在开区间(a，b)内的每点处都可导，则称函数f(x)在开区间(a，b)内可导．

闭区间［a，b］上可导 如果函数f(x)在开区间(a，b)内可导，且f′+(a)及f′－(b)都存在，则称f(x)在闭区间［a，b］上可导，

导函数定义 对于任一x∈I，都对应着f(x)的一个确定的导数值，这样就构成了一个新的函数．这个函数叫做原来函数y=f(x)的导函数，记作

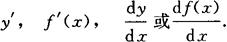
可导与连续的关系定理 函数f(x)在点x₀处可导，则f(x)在点x₀处连续．但逆命题不成立．

函数和、差、积、商的求导法则 设函数u(x)，v(x)均可导，则u(x)±v(x)，u(x)．v(x)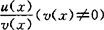，均可导，且

(1)［u(x)±v(x)］′=u′(x)±v′(x)；

(2)［u(x)·v(x)］′=u′(x)v(x)+u(x)v′(x)；

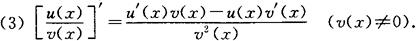
反函数的导数 如果函数x=φ(y)在某区间I_y内单调、可导且φ′(y)≠0，则它的反函数y=f(x)在对应区间I_x内也可导，并且

复合函数的求导法则(链式法则) 如果函数u=φ(x)在点x₀处可导，y=f(u)在点u₀=φ(x₀)处可导，则复合函数y=f［φ(x)］在点x₀处可导，且其导数为

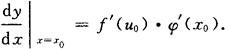
常用导数公式

(c)′=0；

(sinx)′=cosx；

(cosx)′=－sinx；

(tanx)′=sec²x；

(cotx)′=－csc²x；

(secx)′=secxtanx；

(cscx)′=－cscxcotx；

(x^μ)′=μx^μ－1；

(a^x)′=a^xlna(a＞0，且a≠1)；

(sinhx)′=coshx；

(coshx)′=sinhx；

高阶导数定义 如果导函数f′(x)仍然可导，则称f′(x)的导数是函数y=f(x)的二阶导数，记作

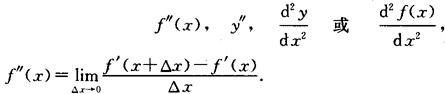
类似地，二阶导数的导数称为三阶导数，记作

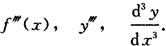
三阶导数的导数称为四阶导数，记作

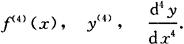
函数f(x)的n－1阶导数的导数叫做n阶导数，记作

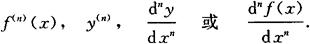
二阶和二阶以上的导数统称为高阶导数．相应地，f(x)称为零阶导数，f′(x)称为

一阶导数．

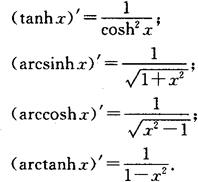
常用高阶导数公式

(a^x)⁽ⁿ⁾=a^x·lnⁿa (a＞0，且a≠1)；

(e^x)⁽ⁿ⁾=e^x；

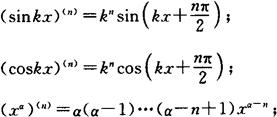
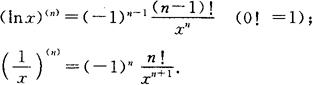
n阶导数的莱布尼茨(Leibniz)公式

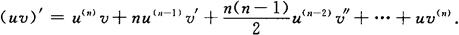
例 y=x²e^2x，求y⁽²⁰⁾．

解 设u=e^2x，v=x²，则

u^(k)=2^ke^2x (k=1，2，…，20)，

v′=2x，v″=2，v^(k)=0 (k=3，4，…，20)

代入莱布尼茨公式，得

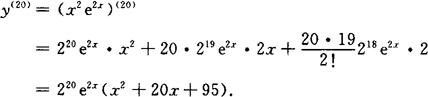
隐函数求导法 用复合函数求导法直接对方程F(x，y)=0两边求导．

例 求由方程e^y+xy－e=0所确定的隐函数y的导数．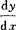

解 方程两端对x求导，得

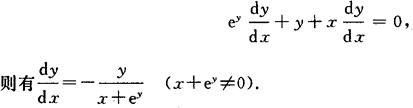
对数求导法 先在方程两边取对数，然后利用隐函数的求导方法求出导数．

对数求导法适用范围 多个函数相乘及幂指函数u(x)^v(x)的情形．

例 f(x)=u(x)^v(x) (u(x)＞0)，求f′(x)．

解 因为 lnf(x)=v(x)·lnu(x)，

所以

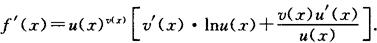
由参数方程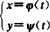所确定的函数的微分法

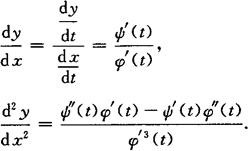
曲线的切线倾斜角与切点和极点的连线间的夹角关系 设已给曲线的极坐标方程为r=r(θ)，则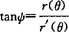(见图3．2)．

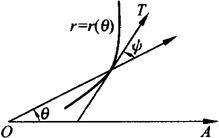
图3．2

相关变化率 设x=x(t)及y=y(t)都是可导函数，变量x与y间存在某种关系，从而变化率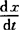与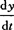之间也存在一定关系．这两个相互依赖的变化率称为相关变化率．