单螺杆挤出成型机的挤出量和机头压力
出处:按学科分类—工业技术 中国轻工业出版社《聚氯乙烯加工手册》第177页(6034字)
已如前说,螺杆的结构或分成三段,塑料在三段上的运行按一定的规律进行。正常情况下,螺杆三段在结构上应该符合下列的要求,即Q1≥Q2≥Q3,Q1为加料段流量,Q2为压缩段流量,Q3为计量段流量,否则就会使挤出量不稳定和质量低劣。这样,计量段就成为整个螺杆挤出量的控制段,也就是挤出成型机的流量等于计量段的流量。但是上式表示的不等情况不能过大,不然计量段会出现超载等不正常情况。
由于塑料在挤出成型机中从固体状态逐步变为粘流态的运动状况较复杂,而且影响挤出成型机生产能力的因素很多,因此,计算挤出成型机生产能力的理论,在目前还不能完全按经验公式或理论公式计算。下面简单介绍理论公式计算法。
(一)进料段的输送能力
下式是一个早期计算挤出成型机生产能力的固体输送公式(纯机械式),它把挤出成型机内的物料看成是一个固体塞子,而把物料的运动看成象螺母在螺杆上移动一样。其表示式为:

式中 Q1——进料段的输送能力(kg/h)
D平均——螺杆、螺纹的平均直径(cm)
φ——螺纹升角
F——螺槽的横断面积(cm2)F=W·h
W——螺槽宽度(cm)
h——螺槽深度(cm)
ρ——塑料密度(g/cm3)
n——螺杆转速(r/min)
β——传送系数
(πD平均/cosφ)F相当于一个螺距内的螺槽容积;传送系数β是修正各个影响因素和可变条件的一个系数。β的实际近似值可根据不同型式的挤出成型机和具体生产条件,通过经验来求得。一般β=0.2~0.4,新机台取大值,旧机台或制造比较粗糙的机台取小值。还可以用下述简化公式计算螺杆进料段的挤出量(固体输送量)。
简化公式(假设物料与螺杆之间的摩擦系数为零):

由于D远大于h,故上式可简化为如下近似式:
Q/n=π2D2hsinφcosφ
当考虑物料与机筒的摩擦时,可用下式计算:

式中 Q/n——进料段的固体输送量(cm/r)
Q′——进料段的固体输送量(kg/min)
ρ——固体物料的体积密度(kg/cm3)
θ——固体料栓相对于机筒的摩擦角(通常为10°~25°)
减小物料与螺杆的摩擦,增大物料与机筒的切向摩擦,则可提高挤出量。
联邦德国IKV塑料研究所改进的挤出成型机进料段结构,使固体输送段的输送效率提高40%~100%,甚至提高到200%。图4-1-12是该结构的示意图。它的最大特点是在进料段设置了一个内壁带有锥度和轴向开有一定形状的沟槽的进料套筒,同时再在套筒外围加设冷却装置。运转时,进料套筒能保证塑料完全填满进料段并将它充分压实,而套筒的轴向沟槽则能防止塑料在此外形成“塑料塞”随同螺杆一起转动,这样的塑料塞完全象一个外缘被夹住的螺母,在一个旋转着的螺钉上向前移动。其输送效率当然就比一般设计的结构高得多。
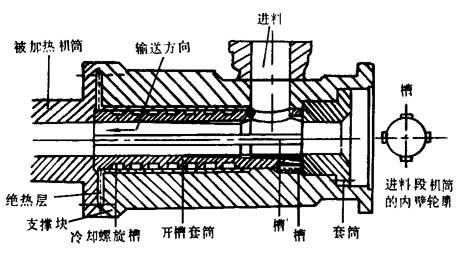
图4-1-12 锥形进料套筒
设置冷却装置为的是防止塑料在进料筒的沟槽内发生熔化,从而失去夹持的作用。此外,为了防止热量从邻近的区段传过来,还应设置绝热层。图4-1-13系该结构α与一般进料的结构b对固体输送效率的比较。

图4-1-13 输送效率比较
进料套筒长度以(3~5)D为多,形状则以锥形较多。夹持塑料的沟槽形状有矩形、锯齿形和镰刀形等多种,其中以镰刀形为多。如果以镰刀形槽和矩形槽相比,则前者的破料效果较后者的缓和。当镰刀形槽的进料效果欠佳时,可采用矩形或锯齿形槽,以及增减槽数来调整。沟槽的数目视具体情况而定,约在6~12的范围内。圆锥形进料套筒的开口斜度约为1°40′左右。
(二)均化段的挤出量
1.计算公式
根据粘性流体流动理论的推导,单螺杆挤出成型机螺杆计量段的挤出量(即挤出成型机的生产能力)可由下列简化式算出:

式中 Q——挤出机的生产能力(体积流量)(cm3/s)
α——正流流量常数
β——倒流流量常数β=πD2hsinφ/12L
y——漏流流量常数y=π2D2δ3εtgφ/12eL
n——螺杆转速(r/min)
η——熔融物料的粘度(kg·s/cm2)
ΔP——螺杆均化段末端与开始处的压力差(kgf/cm2)
D——螺杆直径(cm)h——螺槽深度
φ——螺纹升角(度)〔一般为17°40′,即螺距S=D时〕
L——螺杆均化段的长度(cm)
e——螺棱宽度(cm)
ε——螺杆偏心距的校正系数
(在理想状态下ε=1,在实际使用中常取为1.2)
δ——螺杆与机筒的间隔(cm)
为了简化计算,ΔP常用螺杆末端的物料压力(即机头压力)P来代替,这样计算结果常有一定的误差。
可以看到,系数α、β和y仅与螺杆的结构尺寸有关,因而当螺杆确定后,α、β和y就是常数。如果以Q对P作图,即可得一直线,如图4114中的直线α,其斜率为(-(β+y)/η)。这一直线表达了螺杆的几何特性,故称螺杆的特性线。

图4-1-14 压力P与生产能力Q的关系
a-螺杆特性线 b-机头特性线
此外,由于上式中的第三项(即漏流流量yΔP/η)在δ很小的挤出机中都小于生产能力Q的5%,故常可略去不计。
公式中的粘度η是一个随物料和温度不同而变的系数,对塑料来说,它的数值还随加工时的剪切应力或剪切速率的不同而不同。为便于计算,习惯上都以特定剪切应力与剪切速率下物料所表现的流动阻力,称为有效粘度(以η效表示)或表观粘度。而在实际运算时相当于公式中粘度η的值。由于影响表观粘度的因素很多,难于从理论上求得数据,所以主要还是根据塑料在不同温度下的剪切速率与有效粘度的关系的实验得到,如图4-1-15所示曲线。使用时可按塑料在成型中所处的剪切速率和温度,在曲线图上查出塑料的有效粘度η,然后就将它直接代入公式中的η进行计算。

图4-1-15 PVC剪切速率和有效粘度关系
2.计算示例PVC密度:1.38g/cm3;熔体指数:0.12g/10min。
根据下列已知条件,求SJ150塑料挤出机的生产能力。
已知:螺杆直径D=150mm,螺杆长径比L/D=20,均化段长度L3=1120mm,螺距S=150mm,螺棱宽度e=15mm,螺槽深度h3=4mm,螺杆与机筒间隙δ=0.45~0.65mm,螺杆转速n=7~12r/min,Q=120~200kg/h,N=25~75kW。
求实际产量Q。

①加工硬聚氯乙烯,物料密度ρ=1.35g/cm3,加工温度为149℃。
取n=11r/min=0.184(r/s)
ΔP=300(kg/cm2)
由tgφ=S/πD=150/π×150=0.319得φ=17°40′
②求取有效粘度η效
因螺槽中物料的平均剪切速率为:

间隙中物料的平均剪切速率为

根据剪切速率和物料的温度(149℃),从曲线图4-1-15中查得螺槽中和间隙中的有效粘度分别为:

相当109(kg/h)
计算结果证明,简化法计算误差不大。
(三)通过机头的料流流量
上面讨论了当螺杆旋转时,螺杆对物料的输送能力,但是从螺杆输送来的物料总是通过成型机头才能完成挤出成型的。所以讨论挤出成型机的生产能力时还必须考虑机头的工作压力。
熔融物料通过机头口模流动的流量公式,
Q=K·P/η
式中 Q——通过机头的体积流量(cm3/s)
P——物料通过机头的压力降(kgf/cm2)
K——机头常数(仅与机头的大小和形状有关)
η——熔融物料在机头处的表观粘度(kgs/cm2)
按机头内腔断面的型状,各种机头常数K如下:
圆孔(棒状)机头:K=πR4/8L
扁平(板、模)机头:K=Wh3/12L
管状(管材)机头:K=π(R外+R内)(R外-R内)3/12L
式中 R——圆孔机头半径
W——扁平机头缝口宽度
L——机头口型平直部分的长度
R外·R内——管环状机头的环孔外·内半径
从机头的流动方程可知,这一方程中的Q和P仍然是线性关系,其斜率为K/η,这表达了机头口模的特性,故称机头特性线,如图4114的直线b。
(四)挤出成型机的综合工作点
从图4114所示机头特性曲线可以看出,P增加时,Q也增大,但在螺杆特性曲线中P增加时,Q则降低。当机头压力P等于0时(即没有安装机头时),生产能力Q达最大值Qmax,而当压力P达最大值Pmax时(这等于将机头完全堵塞,这是不允许的),产量Q=0(此时正流流量等于倒流和漏流流量之和)。但挤出成型机的正常工作是配有机头的情况下进行的,因此挤出成型机的生产能力必定是相同的,故挤出成型机的工作点应是螺杆特性曲线与机头特性曲线的交点,即图1-1-14中的A点,此点即为挤出成型机的综合工作点。这就是说,当挤出成型机的螺杆参数、转速、机头的口模都已确定后,该挤出成型机在所给定的条件下正常工作时在A点。因此,挤出成型机的生产能力为Q1,此时的工作压力为P1。
(五)塑料在挤出成型机内的停留时间
下面是塑料在挤出成型机内停留时间的简单推导:

式中 T——平均停留时间(s)
M——整条螺杆螺槽的总容料量(cm3)
V——每一螺槽的容积(cm3)
Z——螺杆全长的螺槽总数
Q——体积流量
但是应该指出,这里的T与实际情况是有出入的,因为塑料的各点速度并不是完全相同的。
(六)挤出机的机头压力实际生产各种制品时采用机头压力的范围见表1-1-13。
表4-1-13 挤出成型机机头压力范围 (MPa)
