测量误差分析
出处：按学科分类—工业技术 北京理工大学出版社《新编液压工程手册下册》第2104页（5337字）
(1)测量误差的分类
由于各种原因，误差是不可避免的。习惯上将测量误差分为系统误差、人为误差和随机误差。
A．系统误差
在一定的条件下，多次重复测量同一参数时，所得测量误差的大小和符号保持不变；或在条件改变时，按一定规律变化的误差就是系统误差。通常造成系统误差的原因有：
工具误差 它是由于测量工具、测量仪器本身不完善所造成的，如仪器本身制造上的误差、表盘刻度不均匀等。
调整误差 主要指的是由于测量仪器调整不当带来的，如指针式仪表的机械零位偏移、仪器本身校验不准确等。
习惯误差 由于测量人的习惯偏向造成的。若采用数字显示和自动打印记录就可避免此误差。
条件误差 在测量过程中，周围环境条件的变化所造成的误差。周围环境条件包括温度、振动、噪声和磁场等因素，所以测量仪器最好是在现场进行动态标定。
方法误差 由于测量方法不完善、不正确造成的误差。如传感器的安装位置及仪表接地方式不正确等。
在实际工作中，系统误差产生的原因是可以查明的。也可以找出系统误差的大小和规律，对测得的数据作出修正。所以说系统误差是可以减小和消除的。但由于它不符合正态分布规律，故不能用增加测量次数的办法来消除。
B．人为误差(或过失误差、粗差)
由于参加试验的人员粗心、过渡疲劳、精神紧张、不会正确地使用仪器或违反操作规程等造成的操作错误、笔误、读数错误以及计算错误等。一般这种误差明显地歪曲了测量结果，且数值较大，还没有一定的规律可循。
C．随机误差
在消除了系统误差和舍弃了人为误差之后，对同一参数多次测量所得数据，在末位或末二位数字上仍有差别，称此误差为随机误差。它没有确定的变化规律，也不能事先估计，其数值时大时小，或正或负。但在足够多次重复测量后，会发现它符合正态分布(或称高斯分布)。因而增加测量次数可使随机误差对测量结果的影响减小。它产生的原因是许多尚未掌握的因素或一时不便于控制的因素的变化造成的。如在节流小孔流量系数的测定实验中，如果对油温不加控制的话，将给测量结果带来系统误差。若对油温进行控制时，比如30±5℃，则油温在25～35℃范围内变化(这是温度控制所允许的误差)。在此范围内，温度的变化是不受控制的，具有随机性。因此将造成油的粘度的随机变化，使所测得的流量系数数值也有微小变化，这就是随机误差。通常产生随机误差的原因有：
·测量仪器本身的允许误差；
·测量方法的不精密性带来的误差。如从示波图上读取数据时的误差等；
·因周围环境条件允许有一定的变化范围所带来的误差。
综上所述，由于系统误差和人为误差是可以消除和避免的，故在对试验数据进行误差分析时，应该是在消除了系统误差和剔除了人为误差之后，只对随机误差进行分析。由于它服从统计规律，所以要用统计理论来处理。
(2)测量误差分析
A．随机误差的正态分布
在对同一参数进行无限多次测量以后，以测量值x为横坐标，且间距△x取得非常小(dx)，以概率密度Pr(xi)／dx为纵坐标。这样在直角坐标上各点连成的一条光滑曲线，叫正态分布曲线如图35．1－10所示。此曲线表示的函数f(x)称为概率密度函数。这是最常见的一种连续型的分布。概率密度函数的表达式为
δ=x－μ
图35．1－10 正态分布曲线
若以δ作为横坐标时，曲线则如图35．1－11所示。由图示曲线可得出几点结论：·小误差比大误差出现的机会多；
图35．1－11 随机误差的正态分布曲线
·对于δ=0的纵坐标而言，曲线是对称的。即是说绝对值相等的正、负误差出现的概率相同。
·δ趋于±∞时，f(δ)=0，即是说大误差一般不会出现。在一定的测量条件下，δ绝对值是不会超过一定界限的，称为误差的有限性。通常规定误差出现的范围是以标准误差σ为单位来衡量的。此范围△称为误差限
△=kσ
由概率论可知，当k=±3时，误差值不在此限内的概率只有0．27%，也就是说不在此范围内的误差值出现的可能性极小。
·因为随机误差的概率密度函数为
当
，这就是随机误差分布曲线的最高点对应的纵坐标值。可见其大小与标准误差σ成反比。σ变化时则曲线的陡度变化，σ愈小则曲线中部升得愈高，两旁下降愈快；σ愈大则曲线变化平缓。这也就表明，曲线愈陡，随机误差极限范围愈小，因而测量值互相之间愈接近，测量的精密度高。由于标准误差σ决定了测量值的散布情况，所以σ是表示测量精密度的重要参数之一。
B．标准误差σ
由于随机误差符合正态分布，正、负大小相等的误差出现的概率相等，也就不可能求得误差的平均值。当测量次数足够多的话，误差之总和必然趋于零。对于等精度的，单个测量值而言，其标准误差
式中δi=xi－μ，但是真值μ未知。根据概率论，可利用测量值的算术平均值
来估计真值μ。此时得到的误差
称为剩余误差或偏差，从而可导出实际应用的根据有限次测量值求取标准误差σ的公式
这就是白塞尔公式；一般测量次数n＜30次。
C．可疑数据的取舍
在实测的数据中往往会发现某一个或几个过大或过小的数；从数值上看它们与其余的测量值相差很大，或明显地偏离其应有的数值；或破坏了其余各数据点连成的平滑曲线的走向等。若是在试验过程中及时发现了这种情况，一般采取重新进行测量的办法，看是否有重复性。若有重复性则保留此数据，否则去掉。试验结束，在处理试验数据时发现这种情况，最好是能分析出明确的物理或工程技术方面的原因，然后再决定其取舍。不应该为某种企图而轻率地舍弃“坏”数据。若没有充分理由，则应该用统计学中可疑数据处理法则来决定取舍。可疑数据舍弃法则比较多，最常用的是莱因达准则，但它比较保守。总之应本着科学和慎重的态度来对待。
D．测量误差的传递
在试验中对许多参数是直接进行测量的，如长度、压力、流量等。但在很多情况下，数据并不是从直接测量而获得，而是在同时对几个参数直接进行测量后，再按一定函数关系进行计算才能得出，这被称为是间接测量。由于各直接测量所得数据都具有一定的测量误差，必然要对计算出的结果产生影响，这就是误差的传递问题。
E．微小误差准则
在误差的传递计算和实际应用中，为了简化，需要忽略部分影响小的误差。衡量可忽略误差的标准就是微小误差准则。
(A)按代数和合成误差时的微小误差准则
因为 εy=∑Dεi=Dε1+Dε2+…十Dεk+…+Dεk其中
；若Dεk项或其中几项之和小到可以忽略的话，设忽略后的计算结果为
。可忽略的条件是
这就是按代数和合成误差的微小误差准则。在一般技术测量中，可放宽为当｜Dεk｜≤0．1εy时就可忽略。
(B)按方和根合成误差时的微小误差准则
因为
其中
i；若Dσk项被忽略，则得到的总误
差为
；可忽略的条件是
，即
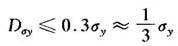
这就是按方和根合成误差时的微小误差准则。在一般技术测量中可放宽为
，Dσk≤0．4σy时，它就可忽略掉。
在测量仪器及系统的标定中，有一项较为重要的工作，也是属于“试验设计”的范畴，就是标准仪器精度等级的选取问题。这就要根据上述微小误差准则，使选定的标准仪器允许的误差对标定结果总误差的影响应小到可以忽略的程度。
设被标定仪器允许误差为rb=a%；
标准仪器的精度级别为rp=A%；
标定结果的误差为r；
根据方和根合成的微小误差准则，当
时，则标准仪器的误差rp对标定结果误差r的影响可以忽略，因而r≈rb。可见：
即 A%≤(1／3)(a%)
这就是一般希望标准仪器的精度比被标定仪器的精度至少要高三倍的理由。
F．误差的分配
在间接测量中，根据误差的传递及合成解决了已知各直接测量值的误差求总误差的问题。若已知或预先规定了测量结果允许的误差范围，要求将此总误差分配到各直接测量的误差中去，以保证达到预定的要求，这就是误差的分配问题。由前述已知，对于随机误差，误差的合成公式为
今σy为已知，是预先规定的。而公式右边的根号下的各直接测量值的误差对总误差的影响项却有若干个，公式只有一个。因而对于各种不同的Dσi的组合都可使σy小于或和等于预定的值。一般误差的分配可按两步进行：
(A)按等影响原则分配。假定各直接测量值的
误差对总误差的影响项均相等，即
Dσ1=Dσ2=…=Dσ6=Dσ
实际上这种等影响的现象是不存在的。按这种分配原则求出的Dσ也是不合理的，只能是作为一次近似和试探。
(B)在已求出的Dσ基础上，根据每个直接测量参数现有的测试水平、仪器设备的发展状况、试验环境、操作难易程度、经济指标以及各直接测量值误差对总误差的影响效果大小等具体情况，对Dσ进行加权调整。以便使测试工作能在既简单、经济，又在实际条件下切实可行的完成，保证实现预定的总误差指标。