几何法设计平面连杆机构
出处:按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第1912页(8609字)
3.1.1 刚体导引机构的设计
如图5.4-2所示,其中的S4(A1B1C1D1)和S2(A2B2C2D2)称为平面S(ABCD)的两个“有限分离”位置。当平面S从位置1作有限分离位移到位置2时,可视为是绕点P12转动而获得的。P12点是A1A2和B1B2(或C1C2和D1D2)的中垂线a12和b12(或c12和d12)的交点,称该交点为平面S有限分离位移的转动极点,简称极点。由A1、A2、B1、B2、C1、C2、D1、D2各点与P12点分别连线,则
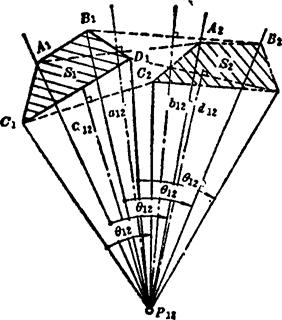
图5.4-2 转动极点
∠A1P12A2=∠B1P12B2=∠C1P12C2=∠D1P12D2=θ12
θ12是平面S绕P12点由S1转到S2的转角。
如图5.4-3所示,为实现连杆平面S两个有限分离位置(S1和S2)的铰链四杆机构,P12点为连杆平面两个有限分离位移的转动极点,则连架杆与机架的铰链中心OA、OB必分别位于中垂线a13和b12上.由图可见:
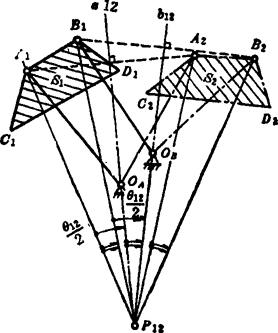
图5.4-3 等视角关系
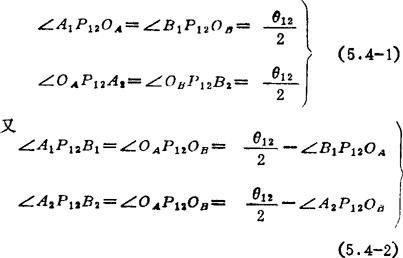
则得等视角定理:转动极点对四杆机构两组互为对
面杆的铰链中心的视角分别相等或互为补角(参见图5.4-4).
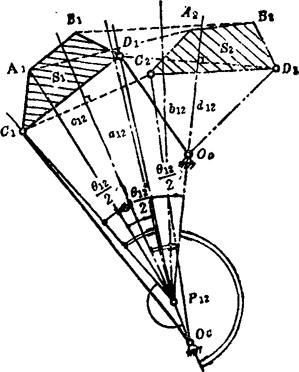
图5.4-4 连杆两个位置的设计
连杆两个位置的设计如图5.4-4所示,其设计步骤如下:
① 由连杆的两个给定位置A1B1和A2B2求出转动极点P12和半角θ12/2(简称∠P12)。
② 令∠P12绕转动极点P12转出两个位置C1P12c12和D12P12d12,并在这两个位置的相应边上,分别任意选取两连架杆连接连杆的铰链中心C1、D1和连接机架的铰链中心Oc、OD,则C1OcODD1即为所求四杆机构的简图。当杆COc从C1Oc转到C2Oc时,连杆平面ABCD就从给定位置A1B1C1D1达到A2B2C2 D2。这类设计问题有无穷多解。
连杆三个位置的设计如图5.4-5所示,其设计步骤如下;
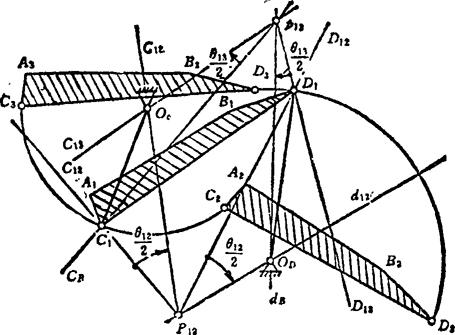
图5.4-5 连杆三个位置的设计
① 任选连杆平面的一个位置作为参考位置,例如第1位置A1B1。
② 由连杆的三个给定位置A1B1、AtB2、A3B3,求出转动极点P12、P13和半角θ12/2、θ13/2(简称∠P12、∠P13——这一步骤未在图中画出)。
③ 在连杆平面上任选一点,为C1,令∠P12和∠P13分别绕转动极点P12和P13转动,使P12c12边和P13c13边交于C1点,则得边P12c12和P13c13的交点Oc。
④ 再选一点D1,用同样方法求出其相应点OD。OcC1D1OD即为所求机构在第1位置的简图。显然,当连杆平面上的C1D1通过C1D1、C2D2和C3D3位置时,其上的A1B1线通过A1B1、A2B2和A3B3。
因为C1和D1都是任选的,故有无穷多解。
连杆四个位置的设计如图5.4-6所示,其设计步骤如下:
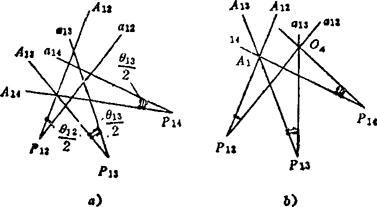
图5.4-6 连杆四个位置的设计
① 选定连杆平面的参考位置,例如第1位置。
② 方法同前,求出P12的位置和∠A12P12a12=θ12/2;P13的位置和∠A13P13a13=θ13/2;P14的位置和∠A14P14a14=θ14/2。为避免图面线条过密,图中未画出连杆平面的四个位置,仅表示出转动极点P12、P13、P14及半角θ12/2、θ13/2、θ14/2。
③ 令P12A12、P13A13、P14A14一组线交于一点,在一般情况下,则另外三边形成的一组线不会交成一点,如图a)所示。如把半角∠P13、∠P14分别绕各自的转动极点P13、P14转动,改变第一组线交点的位置,则第二组线的三个交点就会分散或靠近。从而,总可找到一个位置使两组线同时各自都有一个交点,如图b)中的A1点,称为圆周点(简称圆点),以及OA点,称为圆心点(简称圆心)。这样,就在参考位置上确定了一个圆点A1和相应点圆心OA。
④ 改变∠P12的位置,同样可确定一对相应的圆点和圆心。连续改变∠P12的位置,便可得到一系列的圆点和圆心。把一系列圆点连成曲线,称圆点曲线,以K1表示(圆点曲线的形状参见图5.4-7);由圆心连成的曲线,称圆心曲线,以M1234表示。在K1上任选两圆点,如A1、B1,作为连杆的铰链中心,用等视角关系找出相应的圆心OA、OB作为机架的铰链中心,即可求得所需的机构,可有无穷多解。
圆点曲线是在连杆平面上的平面曲线,它随所取连杆平面参考位置不同而异。以上圆点是在第一位置作出的,故以K1表示。如以连杆平面的第二位置作为参考位置,则应求出转动极点P21、P23、P24和半角∠P21=θ21/2、∠P23=θ23/2、∠P24=θ24/2,且求出的圆点曲线应以K2表示。圆心曲线是在机架平面上的平面曲线,不随连杆平面的参考位置而异,而且只有一条。作圆点曲线和圆心曲线时,可用透明纸做出半角∠P12、∠P13和∠P14的样板,各样板上分别注明符号2P12、A12、a12,P13、A13、a13,P14、A14、a14,再用图钉将样板上的半角顶点P12、P13、P14揿按在图纸的相应的转动极点上,转动样板,使三个样板所形成的两组直线(P12A12、P13A13、P14A14为一组,P12a12、P13a13、P14a14为另一组)各自有一交点(这相当于在图b中使两组线分别交于A1点和OA点)。
例如,如图5.4-7所示,已知四杆机构OAA1B1OB,设计一带近似停歇的六杆机构,其主动杆OAA1转ΦT角时,从动杆ODD1近似停歇,ODD1的摆角为ψ。首先,在ΦT区间选择主动杆OAA1的铰链中心A1的四个位置A1、A2、A3、A4,并求出铰链中心B1的四个对应位置B1、B3、B3、B4。根据连杆的四个位置A1B1、A2B2、A3B3、A4B4可求出圆点曲线K1(K1必通过A1和B1点),并在K1的适当位置选定一点C1,求出与其相应的圆心点D1。然后,以C1D1为杆长,将杆C1D1分别与连杆A1B1C1和从动杆ODD1铰接。当主动杆转 角时,由于连杆的C1点的轨迹近似圆弧,故从动杆ODD1就近似停歇。最后,根据所要求的从动杆的摆角ψ和传动角γ确定OD的位置,从而也就确定了从动杆ODD1的长度。
角时,由于连杆的C1点的轨迹近似圆弧,故从动杆ODD1就近似停歇。最后,根据所要求的从动杆的摆角ψ和传动角γ确定OD的位置,从而也就确定了从动杆ODD1的长度。
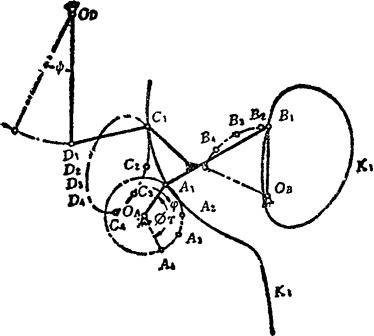
图5.4-7 带近似停歇的六杆机构
连杆五个位置的设计与四个位置的设计解法相同。由于连杆多了一个位置,因此还应求出转动极点P15的位置和半角∠A15P15a15=θ15/2,再用上述样板法试凑,使四个半角两边所形成的两组线(P12A12、P13A13、P14A14、P15A15为一组,P12a12、P13a13、F14a14、P15A15为另一组)各自都有一交点。设A1、OA分别为前后两组线的交点,则A1点就是圆点,OA点就是相应于圆点A1的圆心。连杆平面五个位置的圆点称为“布尔梅斯特n点,其相应的圆心称为“布尔梅斯特”圆心。这种圆点或圆心也可由两条四个位置的圆点曲线或圆心曲线(如1、2、3、4位置和1、2、3、5位置)的交点求得。图5.4-8所示即为由两条圆心曲线的交点求布尔梅斯特圆心的示例。图中两曲线的不与转动极点相重合的交点,即为所求的布尔梅斯特圆心。这种圆心可以有四个,也可以只有两个,或者没有。当两条圆心曲线有四个交点时,如图中的OA、OB、Oc、OD,可得到六个四杆机构,即OAABOB、OAACOc、OAADOD、OBBCOc、OBBDOD及OcCDOD。如只有两个交点,则只有一个四杆机构。无交点时,就没有解。
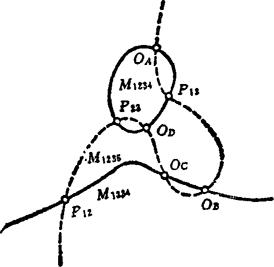
图5.4-8 连杆五个位置的设计
3.1.2 传动机构的设计
相对转动极点示于图5.4-9。在图a)中,两连架杆OAA、OBB由位置1运动到位置2的对应角位移,分别为φ12和ψ12,且均按顺时针方向转动。根据相对运动转换原理,以OAA1为参考位置,则OBB相对于O1A1的第一个位置,即为OBB1,而OBB相对于OAAA的第二个位置。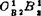 是令OAA2R2OB为一刚体,绕OA反转φ12角,使OAA2与OAA1重合(即作四边形
是令OAA2R2OB为一刚体,绕OA反转φ12角,使OAA2与OAA1重合(即作四边形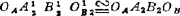 )而获得的。分别作
)而获得的。分别作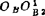 和
和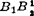 的中垂线,其交点R12即为OBB相对于OAA1运动的相对转动极点。图中
的中垂线,其交点R12即为OBB相对于OAA1运动的相对转动极点。图中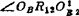 (=
(=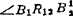 )是OBB相对于OAA1运动的角位移,且等于ψ12-φ12,因而
)是OBB相对于OAA1运动的角位移,且等于ψ12-φ12,因而
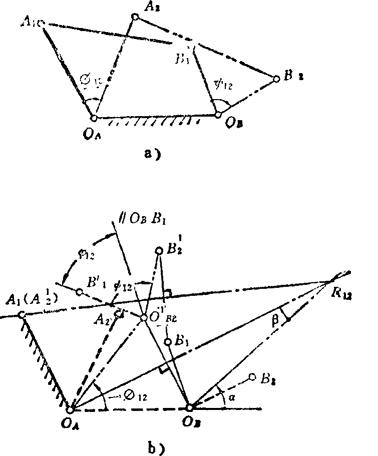
图5.4-9 相对转动极点
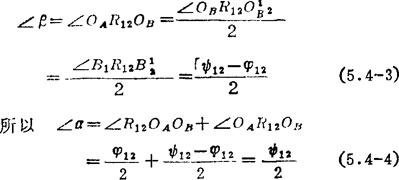
利用上述角的关系,可简便求得R12的位置。如图b),以OA、OB为顶点,按与角位移相反方向从OAOB线起,分别作φ12/2、ψ12/2的角度线OAR12、OBR12,其交点即为相对转动极点R12。
同向转动的两连架杆的一对对应角位移的设计如图5.4-10所示。已知机架铰链中心OA、OB的位置,对应角位移为φ12、ψ12。其设计步骤是:先用φ12/2、ψ12/2值求出相对转动极点R12,过R12点任作直线R12A12、R12B12,使∠A12R12B12=∠OAR12OB=(ψ12-φ12)/2=β,再在R12A12、R12B12上分别任选一点A1和B1作为连杆的两个铰链中心,则OAA1B1OB即为所求四杆机构在第一位置时的运动简图,其两连架杆作同向转动。若需两连架杆异向转动,在选取A1、B1点时,应使A1、B1的连线与OAOB交在OAOB的中间,如图5.4-11所示。由于∠A12R12B12及A1、B1的位置都可以任意选择,故有无穷多解。
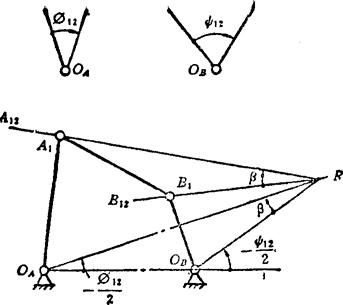
图5.4-10 两连架杆的一对对应角位移(同向转动)的设计
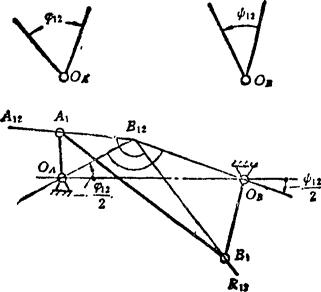
图5.4-11 两连架杆的一对对应角位移(异向转动)的设计
两连架杆的两对对应角位移的设计如图5.4-12所示。已知机架铰链中心OA、OB的位置及两连架杆的两对对应角位移φ12、ψ12和φ13、ψ13,其设计步骤是:先用φ12/2、ψ12/2以及φ13/2、ψ13/2值分别求出相对转动极点R12和R13,然后作∠A12R12B12=∠OAR12OB=(ψ12-φ12)/2,∠A13R13B13=∠OAR13OB=(ψ13-φ13)/2,并令边R12A12和R13A13通过任选的铰链中心A1,则R12B12和R13B13的交点即为另一铰链中心B1的位置。由于A1是任选的,故有无穷多解。
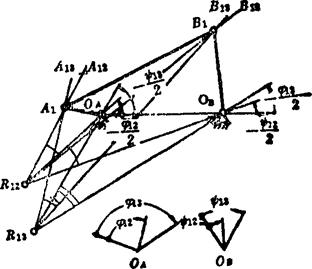
图5.4-12 两连架杆两对对应角位移的设计
两连架杆的三对对应角位移的设计如图5.4-13所示。由于两连架杆的对应角位移只与各杆的相对长度有关,所以机架的铰链中心OA、OB可以任选。在确定三个相对转动极点R12、R13、R14后,即可作作三个半角的样板:∠A12R12B12=∠OAR12OB=(ψ12-φ12)/2;∠A13R13B13=∠OAR13OB=ψ13-φ13/2;∠A14R14B14=∠OAR14OB=(ψ14-φ14)/2。将各样板的顶点绕各自的相对转动极点转动,经过试凑,使三个样板角两边所形成的两组直线(R12A12、R13A13、R14A14为一组,R12B12、R13B13、R14B14为另一组)同时各有一交点,从而确定A1和和B1的位置,求出所需的机构。改变样板的位置,可以得到相对的圆点曲线(通过OB点)和圆心曲线(通过OA点),故仍有无穷多解。
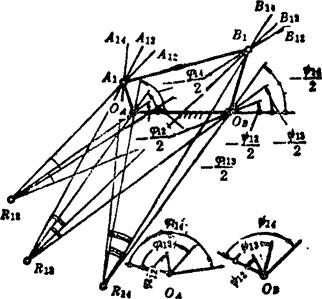
图5.4-13 两连架杆的三对对应角位移的设计
两连架杆四对对应角位移的设计的方法与三对的相同。可先选定机架铰链中心OA、OB,再确定四个相对转动极点R12、R13、R14、R15的位置和四个角度样板∠A12R12R12、∠A13R13B13、∠A14R14B14、∠A15R15B15,然后用试凑法求出连杆铰链中心A1和B1。除OA和OB外,还可能有三对交点,或者是一对,甚至没有。因此,要求实现四对对应角位移或近似实现连续函数时,应预先判断其可能性。
图5.4-14所示为曲柄滑块机构两连架杆的对应位移的设计。已知要求曲柄转角为φ12时,滑块的相应位移为s12。其设计步骤是:首先确定连接曲柄与机架的铰链中心OA的位置和滑块导路的方位。其次求曲柄和滑块的相对转动极点R12。由于滑块作直线运动,故其回转中心OB在垂直于滑块导路方向的无穷远外(见图a)。令以OA为顶点,OAOB为底边,按φ12的反方向作φ12/2的角度线OAR12;同时,从点OA向s12的反方向量取s12/2,并作垂直于导路方向的直线mn,两者的交点即为相对转动极点R12。最后,过R12任意作∠A12R12B12=∠OAR12OB,分别在R12A12和R12B12线上各选一点A1和B1,则OAA1B1即为能满足φ12和s12的曲柄滑块机构在第一位置的简图。

图5.4-14 曲柄滑块机构两连架杆的对应位移的设计
3.1.3 导向机构的设计
极曲线及其几何特性如图5.4-15所示。OAA3B3OB为一曲柄摇杆机构,曲柄圆分为18等份。当铰链A3依次转到A1、A2、……、A18位置时,铰链B3相应运动到B1、B2、……、B18位置。在连杆上取E3和F3点,则描绘出封闭的连杆曲线e和f。显然,当A2在A1、A2、……、A12位置时,连杆E3F3便构成连续的位置列E1F1、E2F2、……、E18F18。根据转动极点的概念,对于连杆位置列中的每两个位置都可以看成是连杆的两个“有限分离”位置,因此可以求出其转动极点:E3F3和E1F1作E3E1和F3F1的中垂线e3.1和f3.1,得转动极点P3.1;E3F3和E2F3作E3E2和F3F2的中垂线e3.2和f3.2,得转动极点P3.2;……;E3F3和E18F18作E3E18和F3F18的中垂线e3.18和f3.18,得转动极点P3.18。把转动极点P3.1、P3.2、……、P3.18连成平滑曲线,便为极曲线(或称转动极点曲线)。由于它们是以连杆第3位置E3F3作为参考位置,而以其他位置E1F1、E2F2、……、E18F18为转动后的位置,故又称为参考位置E3F3的极曲线P3.n(注脚“3”表示参考位置,“n”表示转动后的位置数,即n=1、2、……、18)。
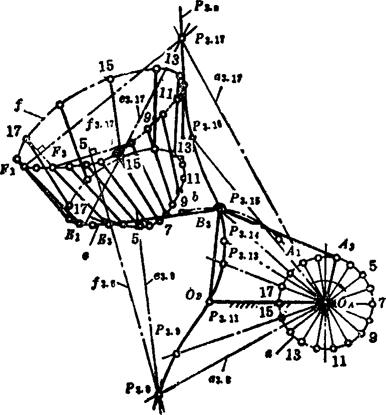
图5.4-15 极曲线
应该指出,极曲线的形状和位置,与参考位置的选择有关。如图5.4-16所示,从曲柄摇杆机构OAA3B3OB的连杆位置列EnFn中,选择E1F1、E3F3、E7F7、E12F12、E15F15等五个位置为参考位置,则可相应画出五条极曲线P1.n、P3.n、P7.n、P12.n、P15.n。虽然这五条极曲线的形状和位置不同,但有其如下的几何特性:1.在曲柄摇杆机构中,不论连杆位置列的极曲线以哪一位置为参考位置,都通过摇杆的固定铰链中心OB点;2.每条极曲线必分别通过对应位置的摇杆活动铰链中心B点。如图5.4-16所示,取连杆位置列中的第三位置为参考位置,则其极曲线P3.n必通过其对应的摇杆活动铰链中心B3点。
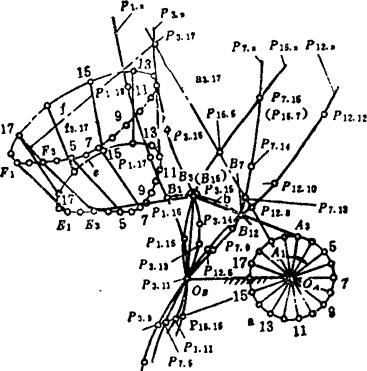
图5.4-16 极曲线的几何特性
采用极曲线设计导向四杆机构,若要求其连杆上的一点实现如图5.4-17中所示轨迹e,则设计步骤如下:
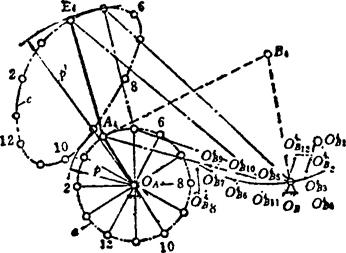
图5.4-17 用极曲线设计导向四杆机构
① 选定曲柄固定铰链中心OA相对于给定的曲线e的位置,则曲柄和连杆的长度lo4A4、lA4E4分别为:
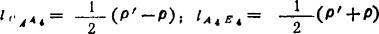
式中 ρ'和ρ为OA至曲线e的最长和最短距离。
② 先在曲柄圆上选A1、A2、……、A12点,并以连杆的长度lA4E4,在曲线e找出E点的相应位置E1、E2、……、E12点,由此求得连杆的位置到A1E1、A2E2、……A12E12。然后从中选择若干位置(一般取4~6个位置)作为参考位置,画出相应的极曲线。
③ 在极曲线比较集中的区域。选取一点作为摇杆固定铰链中心OB(图中只画出OB,未画出极曲线)。
④ 当机构运动时,OB与连杆的相对位置是变化的(如形成△A1E1OB、△A2E2OB、……、△A12E12OB),故需研究OB相对连杆某个位置(如A4E4)的运动。若令A1E1、A2E2、……、A12E12反转至与A4E4相重合,即作全等三角形:
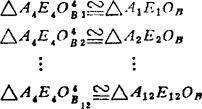
求出相当于连杆在A4E4位置不动的OB的一系列相对位置。
⑤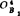 、
、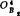 、……、
、……、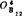 应位于以B4为圆心、lODD4为半径的圆弧上。为此,可利用如图5.4-18所示的找圆心的透明圆弧样板(预先在描图纸上画许多同心圆),覆盖在
应位于以B4为圆心、lODD4为半径的圆弧上。为此,可利用如图5.4-18所示的找圆心的透明圆弧样板(预先在描图纸上画许多同心圆),覆盖在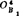 、
、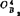 、……、
、……、 点上,找出最逼近这些点的圆,然后用针在圆心上向下戳一小孔,该点就是
点上,找出最逼近这些点的圆,然后用针在圆心上向下戳一小孔,该点就是 ,圆弧半径为loBB4。OAA4E4B4OB就是所求机构。
,圆弧半径为loBB4。OAA4E4B4OB就是所求机构。
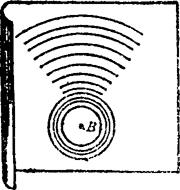
图5.4-18 找圆心的圆弧样板
机构尺寸确定后,绘制运动简图和所实现的连杆曲线e'(图中未画出),检验其误差,并考虑附加要求,比较设计结果,从中选择较优方案。
3.1.4 设计常用的其他几何作图法
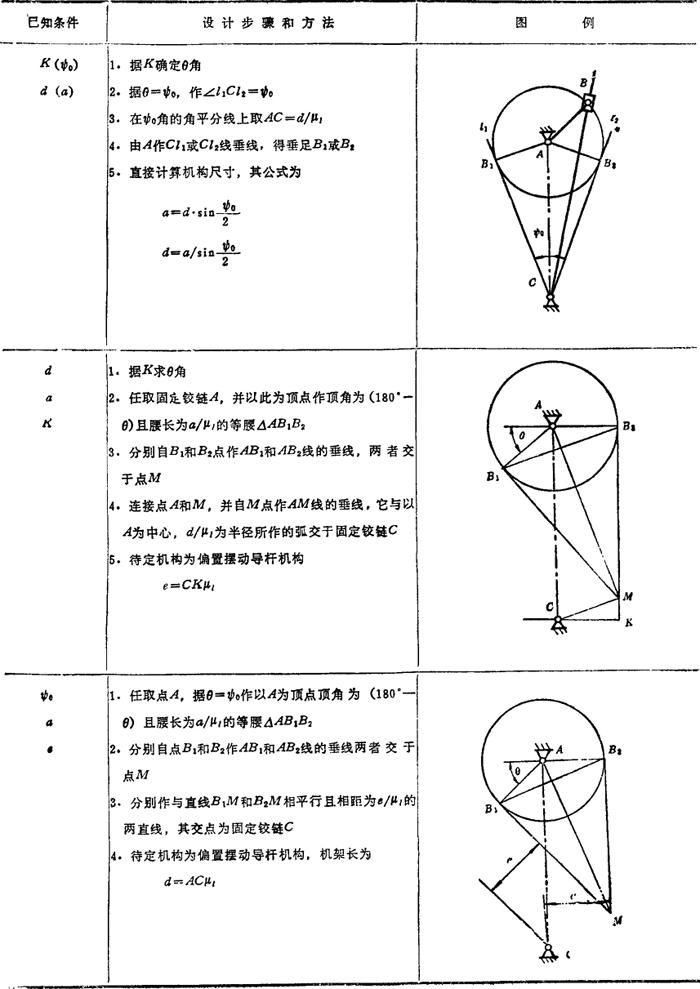
设计中常用的其他几何作图法见表5.4-3~5.4-8。
表5.4-3 曲柄摇杆机构的设计
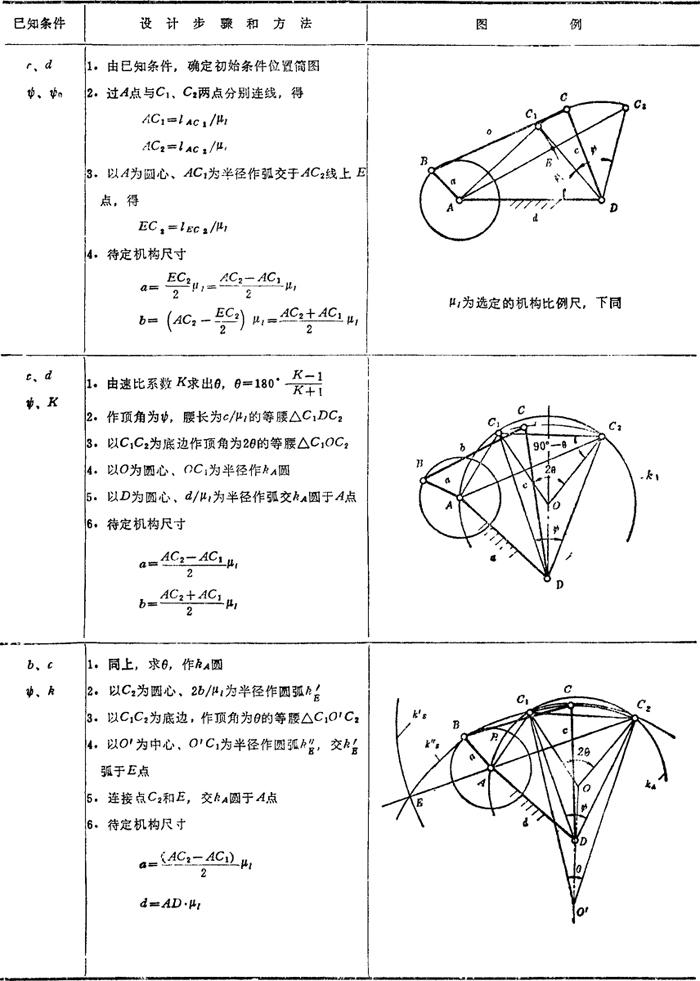
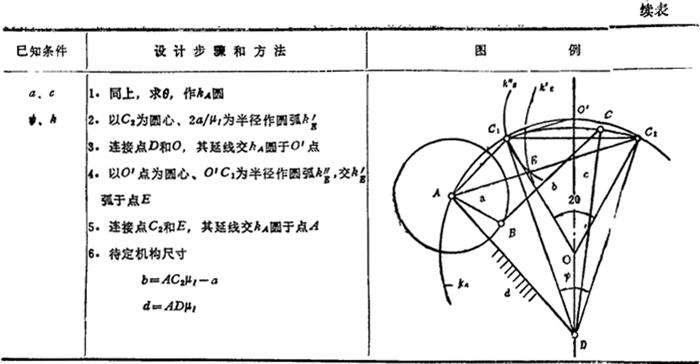
表5.4-4 双曲柄机构的设计
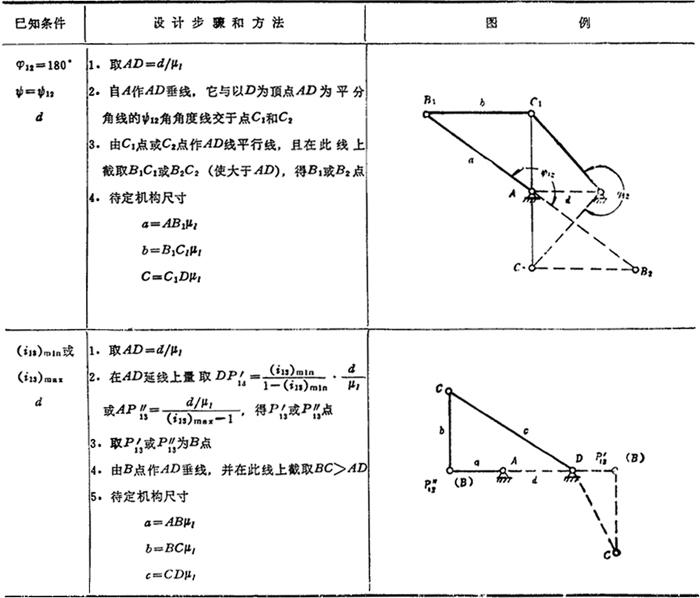
表5.4-5 双摇杆机构的设计
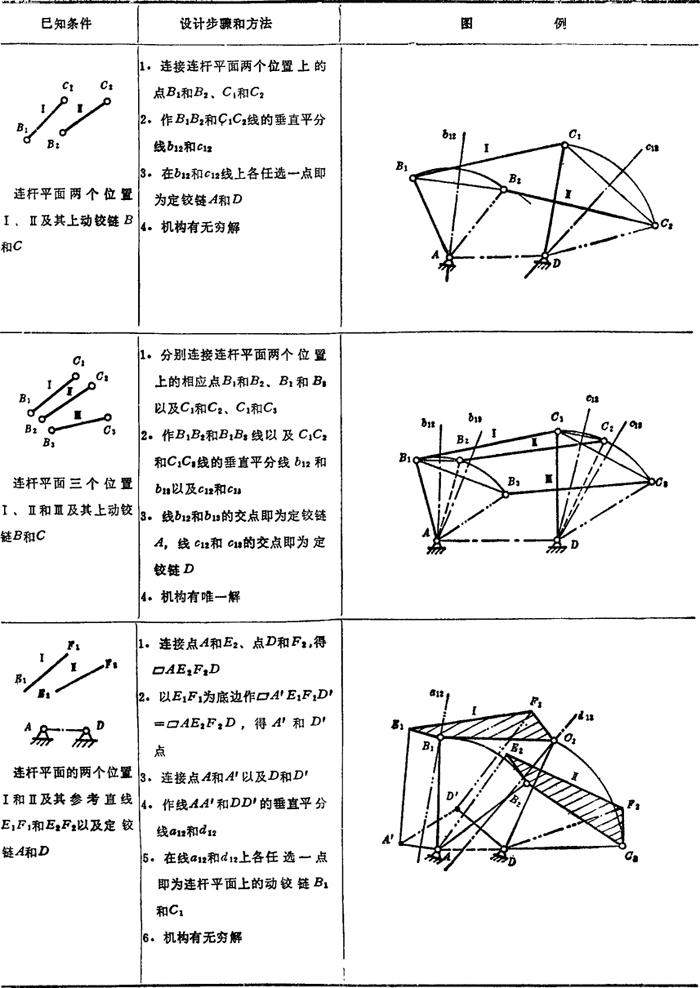
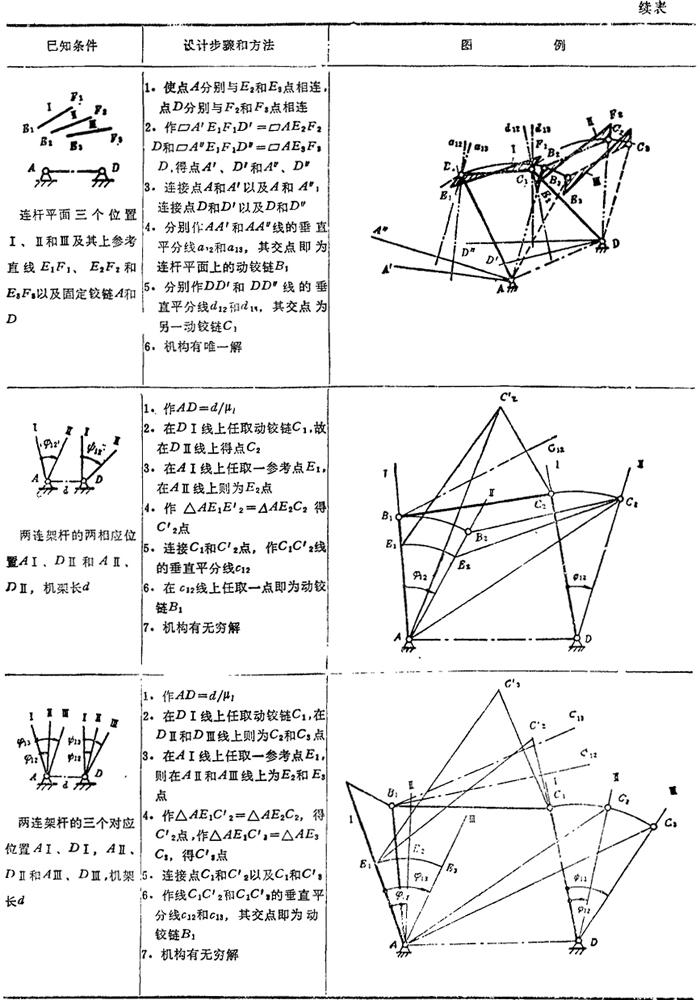
表5.4-6 曲柄滑块机构设计
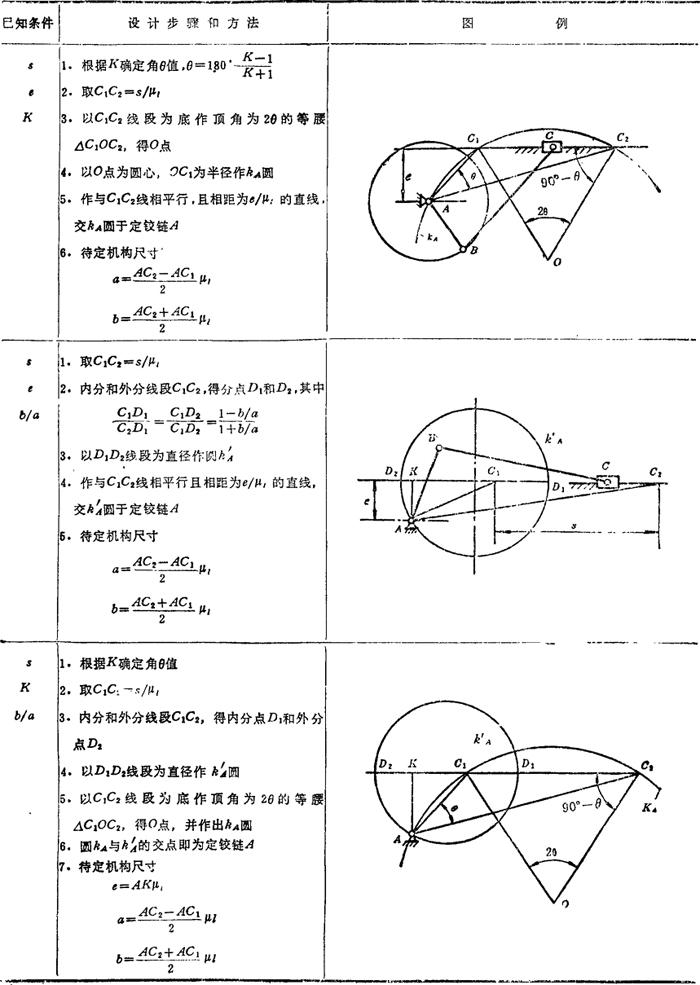
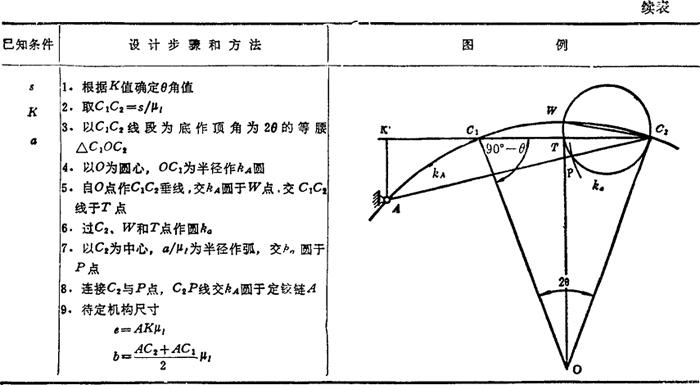
表5.4-7 摆杆滑块机构设计

表5.4-8 摆动导杆机构的设计