连杆曲线的多重生成与同源机构

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册中》第2107页（1430字）

连杆曲线三重发生的罗伯特-契贝雪夫定理：每一条由四杆机构所生成的连杆曲线，都可由另外两个四杆机构生成。这说明，同一连杆曲线可由不同连杆机构连杆平面上的有关点画出，这些机构之间存在着一定尺寸转换关系。这样的能描绘同一连杆曲线的机构族，称为同源机构。同源机构的存在，使得有可能根据较好的运动特性、传动角和位置要求，来选择合适的机构。例如，有一曲柄摇杆机构A₀ABB₀，其连杆平面ABC上C点的轨迹曲线用来达到某个确定的目标，如图5．15-11所示。这一连杆曲线K_c还可由另外两个四杆机构生成。确定另外两个生成同一连杆曲线的四杆机构的尺寸，可借助于辅助图(见图b)。先在任一直线上画出杆长A₀A、AB和BB₀，并在线段AB上根据AC和BC作出连杆三角形ABC。然后过A₀、B₀和C点分别作连杆三角形三个边的平行线，这样就得到另外两个四杆机构A₀EDM₀和B₀FGM₀的尺寸。这些尺寸可转画到位置图(见图Ω)，但预先要定出机架上的支承点M₀。为此可先作三角形A₀B₀M₀，同向相似于连杆三角形ABC。然后作平行四边形A₀ACE和B₀BCF及相似三角形CED和CFG，分别确定E、G、C和F点。于是得到能描绘同一连杆曲线K_c的三个四杆机构A₀ABB0、A₀EDM₀和B₀FGM₀。

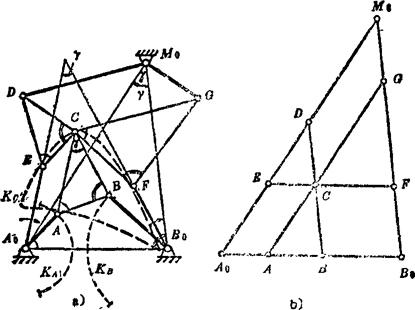
图5．15-11 同源机构尺寸的确定

a)位置图 b)辅助图

由图5．15-11可知，在同源机构中，连架杆A₀E总是与连杆三角形的边AC保持平行，而连架杆B₀F总是与连杆三角形的边BC保持平行。由于连杆三角形的两条边AC和BC的夹角γ是不变的，因而连架杆A₀E和B₀F间的夹角在机构运动的各个位置都保持相等角度γ。这样，在A₀E和B₀F之间可用传动比为1的匀速传动机构连接起来，如用平行四边形机构连接。同样，在连架杆A₀A和M₀G之间以及连架杆M_．D和B₀B之间也都具有相等的角速度。

如图5．15-12，若在连架杆A₀A上选一点H。使A₀H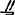M_．G，再在H点用铰链连接杆HI，作CGHI为一平行四边形，于是I点的运动轨迹将与连杆点C描出的连杆曲线K_c全同。应用这一性质，可得到图b)所示的六杆机构，它是在四杆机构A₀ABB₀的连杆点C上添加Ⅱ级组CIH构成的。由于选定H点时满足前述条件，因而铰链点Ⅰ描出一条全同于连杆曲线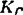的曲线K_j0这就是说，构件CI是沿连杆曲线K_c作平行移动。

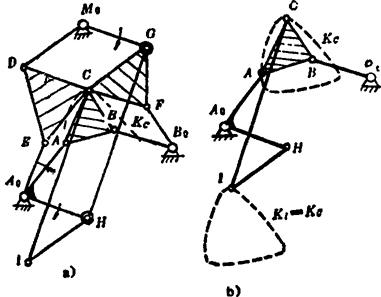
图5．15-12 利用同源机构性质构成的六杆机构

如果连杆三角形退化为直线，也就是A、B、C三点位于一条直线上，如图5．15-13。这时，已不是三角形相似，而是连杆上对应线段成比例。即

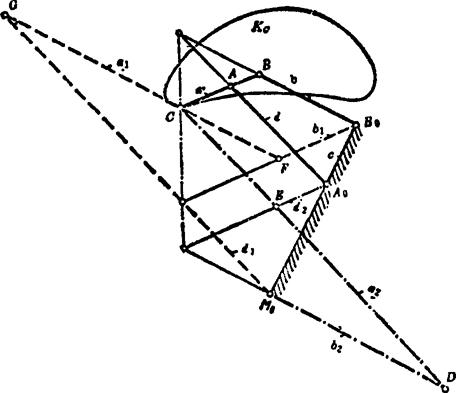
图5．15-13 同源机构尺寸的确定(连杆三角形退化为直线)CF∶CG=BA∶AC；CE∶ED=RA∶AC；B₀A₀∶A₀M₀=BA∶AC。若需求出其同源机构，可在B₀A₀的延长线上按上述比例定出M₀，然后作平行四边形B₀BCF和A₀ACE定出F和E点，最后定出D和G点。于是，便得到能生成同一条连杆曲线的另外两个连杆机构。