常系数线性微分方程

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第28页（954字）

10．2．1 齐次线性微分方程通解的求法

对于n阶实常系数齐次线性微分方程

a0y⁽ⁿ⁾+a₁y^(n－)+…+a_n－1y′+a_n=0(a₀≠0)

所作的n次代数方程

a0λⁿ+a₁λ^n－1+…+a_n－1λ+a_n=0 a₀≠0

称为微分方程的特征方程，其n个根为微分方程的特征根。齐次线性常微分方程的通解可以用它的n个线性无关的特解来表达。表1．1－14列出了齐次线性微分方程的特征根与其对应的线性无关的特解的关系。

表1．1－14 齐次线性常微分方程的特征根与特解的关系

10．2．2 二阶非齐次常系数微分方程的特解

对于微分方程y″+py′+qy=f(x)，根据f(x)的不同类型可归纳其特解形式和求法如下：

①f(x)=P_n(x)(n次多项式)，当q0时，y==Q_n(x)；当q=0时，y=xQ_n(x)。式中Q_n(x)也是n次多项式，其系数用待定系数法求解。

②f(x)=ke^ax(k，a为常数)，当a不是特征方程的根时，；当a是特征方程的单根时，当a是特征方程的重根时，。

③f(x)=Pn(x)e^x(Pn(x)为n次多项式)，当a不是特征方程的根时，=Qn(x)e^ax；当a是特征方程的单根时，=xQ_n(x)e^ax；当a是特征方程的重根时，=x²Q_n(x)e^ax。用待定系数法求解n次多项式Q_n(x)的系数。

④f(x)=ke^axcosβx，或le^axsinβx，或e^ax(kcosβx+lsinβx)，若α±iβ不是特征方程的根时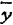，=e^ax(Acosβx+Bsinβx)；若a±iβ是特征方程的根时，=xe^ax(Acosβx+Bsinβx)。式中A、B为特定系数。