稳定判据

出处：按学科分类—工业技术 北京出版社《现代综合机械设计手册上》第395页（4055字）

利用稳定的充要条件可判断系统的稳定性，但这必须了解系统特征根实部符号，即要对方程求根。对于高阶系统，求根工作量较大，故一般不直接利用稳定的充要条件确定系统的稳定性，而是利用稳定判据确定系统的稳定性。

3．2．1 劳斯判据

劳斯判据是一种代数稳定判据。若劳斯表中第一列数均大于零，则系统稳定；如果劳斯表第一列出现小于零的数，则系统不稳定，并且第一列各数符号改变的次数等于特征方程的正实部根的数目。

劳斯表是根据系统闭环特征方程的系数列出的。设系统特征方程为

a_nsⁿ+a_n－1s^n－1+…+a₁s+a₀=0(a_n＞0)

于是可列劳斯表如下：

表中，第一行与第二行是由特征方程的系数直接写出的。第一行由特征方程的第一、三、五…项系数构成，第二行由第二、四、六…项系数构成，第三行(s^n－2行)各数b_i(i=1，2…)由下式算出：

一直计算到b_i=0为止，第四行(s^n－3行)各数c_t(i=1，2，…)由下式算出：

一直计算到c_t=0为止，第五行及第五行以后各行可按式(1．9－29)和式(1．9－30)给出的计算方法递推计算，一直计算到第n行(s′行)。第n+1行(s0行)仅第一列有数，并且等于特征方程最后一项系数ao。

例1．9－10 已知系统的特征方程为

s⁵+4s⁴+8s³+9s²+6s+2=0

试用劳斯判据判断系统的稳定性。

解：列劳斯表

表中第一列数均大于零，故系统稳定。

例1．9－11 已知系统特征方程为

s⁶+6s⁵+2s⁴+18s³+5s²+24s+20=0

试判断系统的稳定性。

解：列劳斯表

由于第一列数不全为正，故该系统不稳定，第一列数中从6→－1－4，或从1→－1－1处符号变化两次，故系统特征方程有两个正实部根。

由例1．9－11可知，在计算过程中，用正数去乘(或除)同一行各数，对判断系统稳定性无影响，但可简化计算，

若劳斯表中，某一行第一个数为零，该行其余不全为零时，可用任意小的正数ε来代替这个零，继续计算表中其它行的数，最后取ε→0的极限，利用劳斯判据进行判断，

例1．9－12 已知系统特征方程为

s⁴+s³+2s²+2s+3=0

试判断系统的稳定性，

解：列劳斯表

当ε→0时，(2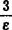－)→－∞，系统不稳定，表中第一列数变号两次，故系统特征方程有两个正实部根。

3．2．2 奈魁斯特判据

奈魁斯特稳定判据简称奈氏判据，是利用开环频率特性和开环极点(即令开环传递函数分母等于零求得的根)情况判断闭环系统是否稳定的一种判据。利用奈氏判据不仅可确定系统是否稳定，而且可得知改善系统稳定性的途径。

(1)利用开环幅相图的奈氏判据

利用开环幅相图判断闭环系统稳定性的奈氏判据可叙述如下；

闭环系统稳定的充分必要条件：

式中 N为开环幅相曲线逆时针包围复平而上(－1，j0)点的圈数，在沿ω增加方向，开环幅相曲线逆时针包围(－1，j0)点取正值，顺时针包围(－1，j0)点则N取负值；P为开环右极点数，即位于S复平面右半平面的开环极点数，如果系统无开环右极点，则闭环系统稳定的充分必要条件是开环幅相曲线不包围(－1，j0)点。若闭环系统不稳定，其闭环右极点数即闭环特征方程正实部根的数目z可由下式求出：

Z=P－2N

当系统开环传递函数中含有γ个积分环节时，绘制开环幅相频率特性曲线后，还应从频率ω=0⁺对应的点开始，逆时针方向用虚线补画一条半径为无穷大、角度为”的圆弧，即系统的开环幅相频率特性曲线由原来的实线和补画的虚线两部分构成。这样，就可利用奈氏判据判断这类含有积分环节的系统的稳定性。

例1．9－13 已知两单位反馈控制系统的开环传递函数分别为

其开环幅相曲线分别如图1．9－28(a)、(b)所示，试用奈氏判据分别判断对应的闭环系统的稳定性。

图1．9－28 系统的开环幅相图

解：对系统1，由开环传递函数G₁(s)的表达式可知P=0；由图1．9－28(a)可知N=0，则N=P／2=0，系统1稳定。

对系统2。由开环传递函数G_d(s)的表达式可知P=0；由图1．9－28(b)可知N=－1，则，系统2不稳定，其闭环右极点数Z=P－2N=0－2×(－1)=2．

例1．9－14 单位反馈控制系统的开环传递函数为

开环幅相频率特性曲线如图1．9－29所示，试判断系统的稳定性。

解：由G(s)表达式及图1．9－29可知，P=1、N=1／2。根据奈氏判据，有N=P／2=1／2．故闭环系统稳定。

图1．9－29 系统开环幅相图

此例说明，开环系统有不稳定环节时，闭环系统仍有可能是稳定的。

例1．9－15 已知系统的开环传递函数

试用奈氏判据判断闭环系统的稳定性。

解：根据开环传递函数绘制的开环幅相频率特性曲线如图1．9－30所示，由图可知N=－1，由G(s)表达式可知P=0，则，系统不稳定，闭环右极点数Z=P－2N=2。

图1．9－30 系统开环幅相图

(2)利用开环对数坐标图的奈氏判据

穿越的概念：在对数坐标图上，在开环对数幅频特性曲线L(ω)的正值区间，沿ω增加方向，对数相频特性曲线φ(ω)自下向上穿过－180°线为正穿越，其数可用N₊表示；沿ω增加方向，对数相频特性曲线φ(ω)自上向下穿过－180°线为负穿越，负穿越数可用N－表示。如图1．9－31所示曲线中，1点的穿越是负穿越一次，2点的穿越是正穿越一次。

图1．9－31 对数坐标图

利用开环对数频率特性曲线判断闭环系统稳定性的奈氏判据也称对数频率稳定判据。其闭环系统稳定的充要条件是，在开环对数幅频特性曲线L(ω)的正值区间，开环对数相频特性曲线φ(ω)对一180°线的正穿越数与负穿越数之差N等于开环传递函数右极点数P的一半，即

若闭环系统不稳定，其闭环右极点数为

Z=P－2N

若开环传递函数中含有积分环节，在对数相频特性曲线上要做与开环幅相频率特性曲线上相应的处理(即补线)，然后再使用对数频率稳定判据判断系统的稳定性，

例1．9－16 已知系统的开环传递函数为

试用对数顷率稳定判据判断闭环系统的稳定性。

解：根据开环传递函数绘制的开环对数坐标图如图1．9－32所示，由于该系统开环传递函数中含有两个积分环节，因此在开环对数相频特性曲线上ω为O⁺处补画一条－180°到0°的虚线。这样，对数相频特性曲线应由虚线和原来的实线构成。由图可知，在L(ω)＞0区间，φ(ω)曲线穿越－180°线的正、负穿越数之差为

N=N₊－N_－=0－1=－1

由G(s)表达式可知P=0．由于，故闭环系统不稳定，其右极点数Z=P－2N=2。

图1．9－32 例1．9－16 系统对数坐标图