指数函数的图象及性质
书籍:高中数理化公式定理大全
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第20页(1111字)

例1 (1)比较(0.034)—0001与634—01的大小;
(2)若a=0.2—3/4,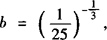 ,c=
,c=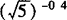 ,则a,b,c的顺序关系如何?
,则a,b,c的顺序关系如何?
解 (1)由指数函数的性质知(0.034)—0001>1,634—0.1<1,所以(0.034)—0001>634—01.
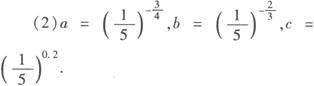
因为0<1/5<1,可知函数y=(1/5)x是减函数,0.2>—2/3>—3/4.
所以a>b>c.
例2 求下列函数的值域及单调区间
①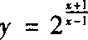 ;
;
②y=(1/3)x2—2x—3.
解 ①由x—1≠0得函数的定义域为{x|x∈R且x≠1}.
设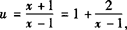 ,则u∈R且u≠1.
,则u∈R且u≠1.
∴函数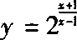 的值域为{y|y>0且y≠2
的值域为{y|y>0且y≠2
∵x∈(—∞,1)时,u为减函数,
x∈∈(1,+∞)时,u为减函数,
又∵y=2x为增函数,
∴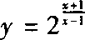 在(—∞,1)、(1,+∞)上都是减函数.
在(—∞,1)、(1,+∞)上都是减函数.
②函数的定义域为R.
设u=x2—2x—3=(x—1)2—4≥—4.
∴0
即函数的值域为{y|0 ∵x∈(—∞,1]时,u为减函数, x∈[1,+∞)时,u为增函数, 又∵ y=(1/3)x为减函数, ..y=(1/3)x2—2x—3的减区间为[1,+∞)增区间为(—∞,1].
上一篇:有理数指数幂的运算法则
下一篇:对数的运算法则