对称轴平行于坐标轴的圆锥曲线
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第85页(1167字)
1.方程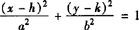 (a>b>0)表示中心在(h,k),对称轴平行于坐标轴的椭圆,其焦点坐标为(±c+h,k),准线方程为
(a>b>0)表示中心在(h,k),对称轴平行于坐标轴的椭圆,其焦点坐标为(±c+h,k),准线方程为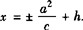 .
.
2.方程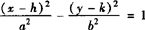 表示中心在(h,k),对称轴平行于坐标轴的双曲线,其焦点坐标(±c+h,k),准线方程
表示中心在(h,k),对称轴平行于坐标轴的双曲线,其焦点坐标(±c+h,k),准线方程 +h.
+h.
例1 平移坐标轴,把原点平移到O′(—1,2),求:
(1)点M(3,4)的新坐标;
(2)在新坐标系中,点N(3,4)的原坐标;
(3)曲线x2+y2+2x—4y+1=0在新坐标系中的方程.
解(1)由移轴公式得
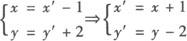
把x=3,y=4代入得x′=3+1=4,y′=4—2=2,所以点M的新坐标是(4,2).
(2)将x′=3,y′=4直接代入移轴公式
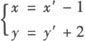
得x=3—1=2,y=4+2=6,∴点N的原坐标为(2,6).
(3)将移轴公式x=x′—1,y=y′+2代入已知方程,得(x′—1)2+(y′+2)2+2(x′—1)—4(y′+2)+1=0.化简整理,得x′2+y′2=4,此即为曲线在新坐标系中的方程.
例2 双曲线3x2—y2=k的中心在直线l∶y=x上移动,且保持对称轴平行于坐标轴,问平移中是否存在这样的双曲线,它截直线l的弦长与截y轴的弦长都等于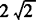 ?若存在,求出双曲线方程,若不存在,说明理由.
?若存在,求出双曲线方程,若不存在,说明理由.
解 设双曲线方程为3(x—m)2—(ym)2=k. ①
将y=x代入,得2(x—m)2=k,
当k≥0,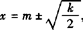 ,双曲线在l上截得的弦长为
,双曲线在l上截得的弦长为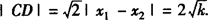 .
.
在双曲线方程①中令x=0,得y2—2my2m2+k=0.
双曲线方程①在y轴上截得的弦为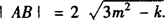 .
.
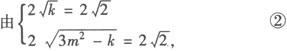
解得k=2,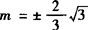 均适合②所以存在符合条件的双曲线,其方程为3(x+
均适合②所以存在符合条件的双曲线,其方程为3(x+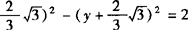 或
或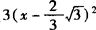
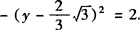 .
.