两个平行平面间的距离
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第95页(2445字)
两平行平面的公垂线段的长度叫做两个平行平面间的距离.
定理4 夹在两个平行平面间的平行线段相等.
定理5 经过平面外一点有且只有一个平面和已知平面平行.
例1 已知a、b是异面直线,且a⊥b,a⊥α,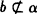 ,求证b∥α.
,求证b∥α.
策略 利用平面平行的性质,证线面平行和利用线线平行证线面平行.
证法一 如图(1)过b上一点P作a的垂线PQ,b与PQ确定平面β.
∵a⊥b,a⊥PQ,∴a⊥β,
又∵a⊥α,∴α∥β,且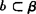
∴b∥α.
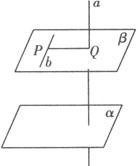
(1)
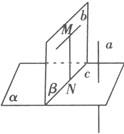
(2)
证法二 如图(2),在b上任取一点M,作MN⊥α于N,直线b与MN确定一个平面,设为β.
∵a⊥α,MN⊥α,
∴a∥MN.
又a⊥b,
∴b⊥MN.
设α∩β=c,且MN⊥α,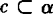 ,
,
∴MN⊥c.
又∵MN⊥b,MN⊥c,且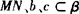 ,
,
∴b∥c,而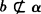 ,
,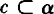 .
.
∴b∥α.
点评 (1)证法一用面面平行的性质证线面平行,这是线面平行的又一个判定定理,方法是构造一个平面β,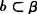 ,易证β∥α.
,易证β∥α.
(2)证法二用线面平行的判定定理,在平面α内可找到一直线c,直线c∥b.
例2 如图,棱长为a的正方体ABCDA1B1C1D1.
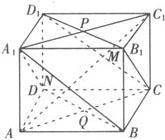
(1)求证:平面A1BD∥平面CD1B1
(2)求平面A1BD和平面CD1B1的距离.
策略 前面例中已给出证明,下面用线面“垂直”关系给出另一种证明,这样利于找到平行平面的公垂线段,进而求出距离.
证及解 设P、Q分别是正方形A1B1C1D1和ABCD的中心,连接AC1,和平面CD1B1相交于M和平面A1DB相交于N.
∵平面ACC1A1∩平面CD1B1=CP,
∴M∈CP.
同理N∈A1Q.
∵CC1⊥平面A1B1C1D1,∴CC1⊥B1D1.
∵A1C1⊥B1D1,∴B1D1⊥平面ACC1A1.
∴B1D1⊥AC1.
同理B1C⊥AC1,∴AC1⊥平面CB1D1.
同理AC1⊥平面A1BD.
∴平面CB1D1∥平面A1BD.
于是,AC1是平面A1BD和平面CB1D1的公垂线,MN的长度就是平面A1BD和平面CB1D1的距离.
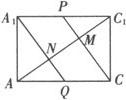
在上图所示的矩形ACC1A1中计算NM的长度.
∵AA1=CC1=a,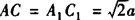 ,
,
∴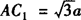 .
.
∵P是A1C1的中点,Q是AC的中点,
∴CP∥A1Q,PM是△C1A1N的中位线.
∴C1M=MN.
同理AN=MN,即M、N是AC1的三等分点.
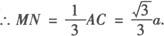
故平面A1BD和平面CD1B1的距离是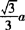 .
.
点评 把空间图形的问题转化为平面图形问题是立体几何解题的一种基本技能,这种降维处理是解决立体几何问题的重要思维方法,本题将对角面移出,不仅使图形得到简化,又能还其图形的本来面貌.
探索 ①异面直线A1B、B1C间的距离为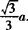 .
.
②点A到平面A1BD的距离为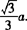 .
.
③AC1与平面AB1所成角的余弦值为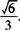 .
.
④CB1与平面AC1所成角的余弦值为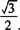 .
.