二项分布
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第112页(1230字)
在一次随机试验中,某事件可能发生也可能不发生,在n次独立重复试验中这个事件发生的次数是一个随机变量,我们知道,如果在一次试验中某事件发生的概率是P,那么,在n次独立重复试验中这个事件恰好发生k次的概率是P(ξ=k)= ,其中k=0,1,2,…,n,q=1—p,于是得到随机变量ξ的概率分布如下:
,其中k=0,1,2,…,n,q=1—p,于是得到随机变量ξ的概率分布如下:

称这样的随机变量ξ服从二项分布,记作ξ~B(n,p),其中n,p为参数,并记 .例如,重复抛掷一枚硬币n次,得到正面向上的次数x服从二项分布,即x~B(n,1/2).
.例如,重复抛掷一枚硬币n次,得到正面向上的次数x服从二项分布,即x~B(n,1/2).
例1 某射手每次射中目标的概率是0.8,连续一个目标射击,直到第一次击中目标为止,求所需射击次数ξ的概率分布.
解 射手连续射击一个目标,击中即止,所需射击次数是一个离散型随机变量,其可能取值为1、2…n、…,每个取值的概率可由乘法原理求得.
射手连续射击一个目标,击中为止,所需射击次数ξ的可能取值为1、2、3、…、n、….
当第n次击中目标时,则前面连续n—1次均未击中目标,此时P(ξ=n)=(0.2)n—1(0.8)(n=1,2,…).
∴ξ的概率分布为

例2 某班学生45人,其中O型血的人有10人,A型血的人有12人,B型血的人有8人,AB型血的人有15人,现抽一个,其血型是一个随机变量ξ,(1)ξ的可能取值是什么?(2)ξ的分布列是什么?
解 (1)将四种血型编号;O、A、B、AB型的编号1,2,3,4则ξ的可能取值为1,2,3,4.(2)当ξ=1,2,3,4时, ,
, ,
, ,
, ,故其分布列为
,故其分布列为

思考 上题中若抽取两人:
(1)求这两人血型相同的概率;
将四种血型编号O、A、B、AB型编号为1、2、3、4则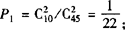 ;P
;P ;
; ;
;

(2)求这两人血型相同的分布列.
将四种血型O、A、B、AB型编号为1、2、3 4记η为两人血型相同,这一随机事件其值可取1、2、3、4,其分布列为
