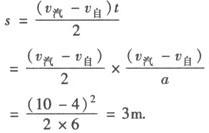匀变速运动规律的应用
出处:按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第170页(3457字)
1.在匀变速直线运动的两个基本规律中,消去时间t,即可得到:vt2—v02=2as.在一个匀变速直线运动的过程中,如果时间未知时,应用此式求解比较方便.
2.在匀变速直线运动中,在连续相邻相同时间内位移差为一常数,等于加速度与时间平方的乘积,即△s=at2.
3.在初速度为零的匀加速直线运动中,有:
(1)1T秒末、2T秒末、3T秒末……的速度比:v1∶v2∶v3∶……vn=1∶2∶3……n
(2)1T秒内、2T秒内、3T秒内……的位移比:S1∶S2∶S3∶……Sn=12∶22∶32∶……n2
(3)第1个T秒内、第2个T秒内、第3个T秒内……(连续相等时间内)的位移比:
SⅠ∶SⅡ∶SⅢ∶……SN=1∶3∶5∶……(2N—1)
(4)通过第1个L、通过第2个L、通过第3个L……(通过连续相等位移)的所用时间比:
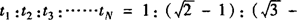
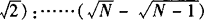
4.在匀变速直线运动中,某段位移中点的速度和某段时间中点的速度分别为:
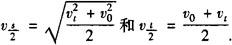
5.将匀减速直线运动等效为反向的初速度为0的匀加速直线运动,有时会极大地减少运算量,达到迅速解题的目的.
例1 有一个做匀变速直线运动的质点,它在两段连续相等的时间内通过的位移分别是24m和64m,连续相等的时间为4s,求质点的初速度和加速度大小.
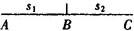
分析 依题意画草图如图所示.
(1)常规解法:由位移公式得
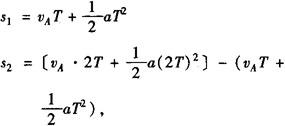
将s1=24m,s2=64m,T=4s代入两式求得vA=1m/s.a=2.5m/s2.
(2)用平均速度求解:
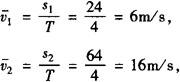
又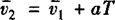 即16=6+a×4,得a=2.5m/s2,再由s1=vAT+1/2aT2求得vA=lm/s.
即16=6+a×4,得a=2.5m/s2,再由s1=vAT+1/2aT2求得vA=lm/s.
(3)用平均速度求解:
设物体通过A、B、C三点的速度分别为vA、vB、vC.
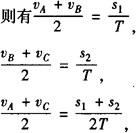
解得vA=1m/s,vB=11m/svC=21m/s所以,加速度为
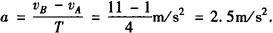
(4)用推论公式求解:
由s2—s1=aT2得64—24=a·42,
所以a=2.5m/s2,代入s1=vAT+1/2aT2,
可求得vA=1m/s.
6.追击与相遇问题
追击、相遇是运动学中研究同一直线上两个物体的相对运动时常常涉及到的两类问题,也是匀变速直线运动规律在实际问题中的具体应用.
1.追击、相遇问题的特征:
追击的主要条件是两个物体在追赶过程中处在同一位置,常见的情形有三种:一是初速度为零的匀加速运动的物体甲追赶同方向的匀速运动的物体乙时,一定能追上,在追上前两者有最大距离的条件是两物体速度相等;二是匀速运动的物体甲追赶同方向做匀加速运动的物体乙时,存在一个恰好追上或恰好追不上的临界条件是两物体速度相等,此临界条件给出了一个判断此种情形能否追上的方法,可通过比较两物体处在同一位置的速度大小来分析,具体方法是:假定在追赶过程中两者能处在同一位置,比较此时的速度大小,若甲的速度大于乙的速度则能追上,反之则追不上,如果始终追不上,当两物体速度相等时,两物体的间距最小;三是匀减速运动物体追赶同方向的匀速运动物体时,情形跟第二种相类似.
两物体恰能相遇的临界条件是两物体处在同一位置时,两物体的速度恰好相同.
2.分析追击相遇问题应注意:
(1)分析追击相遇问题时,一定要抓住一个条件,两个关系:一个条件是两个物体的速度满足的临界条件,如两物体距离最大、最小,恰好追上或恰好追不上等.两个关系是时间关系和位移关系.其中通过画草图找到两个物体位移之间的数量关系,是解题的突破口.
(2)若被追赶的物体做匀减速运动,一定要注意追上前该物体是否停止运动.
(3)仔细审题,注意抓住题目中的关键字眼,充分挖掘题目中的隐条件.如:“刚好”、“恰好”、“最多”、“至少”等,往往对应一个临界状态,满足相应的临界条件.
3.解追击相遇问题的思路
解题的基本思路是:①根据对两物体运动过程的分析,画出物体的运动示意图;②根据两物体的运动性质,分别列出两个物体的位移方程,注意要将物体运动时间的关系反映在方程中;③由运动示意图找出两物体位移间的关系方程;④列方程求解.
4.解决追击和相遇问题的方法有很多,如数学方法、物理方法、图象方法等.
例2 汽车正以10m/s的速度在平直的公路上前进,突然发现正前方有一辆自行车以4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做加速度大小6m/s2的匀减速运动,汽车恰好不碰上自行车,求关闭油门时汽车离自行车多远?
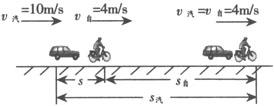
分析 汽车在关闭油门减速后的一段时间内,其速度大于自行车的速度,因此汽车和自行车之间的距离在不断缩小,当这个距离缩小到零时,若汽车的速度减至与自行车相同,则能满足题设的汽车恰好不碰上自行车的条件,所以本题要求的汽车关闭油门时离自行车的距离s,应是汽车从关闭油门减速运动,直到速度与自行车速度相等时发生的位移s汽与自行车在这段时间内发生的位移s自之差,上图所示.
解法1 汽车减速到4m/s时发生的位移和运动的时间分别为

这段时间内自行车发生的位移
s自=v自t=4×1=4m.
汽车关闭油门时离自行车的距离
s=s汽—s自=7—4=3m.
解法2 利用v—t图进行求解,如下图所示,直线Ⅰ、Ⅱ分别是汽车与自行车的运动图线,其中划斜部分的面积表示当两车车速相等时汽车比自行车多发生的位移,即为汽车关闭油门时离自行车的距离s.图象Ⅰ的斜率即为汽车减速运动的加速度,所以应有