两个直线运动的合运动的性质和轨迹的判断方法

出处：按学科分类—文体、科学、教育 商务印书馆国际有限公司《高中数理化公式定理大全》第187页（2572字）

根据平行四边形定则，求出合运动的初速度v₀加速度a后进行判断：

(1)若a=0(分运动的加速度都为零)，物体沿合初速度v₀的方向做匀速直线运动．

(2)若a≠0且a与v₀的方向在同一直线上，物体就做直线运动；a与v₀同向时做加速直线运动；a与v₀反向时先做减运动，当速度减为零后将沿a的方向做加速运动；a恒定时，物体做匀变速直线运动．

(3)若a与v₀的方向不在同一直线上，则合运动是曲线运动，a恒定时，是匀变速曲线运动

例1 已知某船在静水中的速率为v₁=4m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为d=100m，河水的流动速度为v₂=3m/s，方向与河岸平行．(1)今欲使船以最短时间渡过河去，航向怎样?最短时间是多少?到达对岸的位置怎样?船发生的位移有多大?

(2)欲使船以最短位移过河，航向又怎样?渡河所用时间是多少?

(3)若水流速度v₂=5m/s，船在静水中速率v₁=4m/s不变，船能否垂直河岸渡河?欲使船渡过河去的航程最短，航向怎样?最短航程是多少?

分析 船同时参与了这样两个运动：①船相对于水的运动，其速度就是船在静水中的速度v₁=4m/s，方向与船头的指向相同；②船随水漂流的运动，其速度等于河水流速v₂=3m/s，方向平行于河岸，与水流动方向相同，指向下游，船在河水中实际发生的运动(站在岸边的观察者看到的运动)即是由上述两个运动合成的．

解 (1)根据运动的独立性和等时性，从题中已知河宽d=100m的条件出发分析知，当船在垂直河岸方向上的分速度v₁最大时，渡河所用时间才最短，设船头斜向上游且与上游河岸夹角α，其合速度v与分运动速度v₁、v₂的矢量关系如图1所示，河水流速v₂平行于河岸，不影响渡河快慢，船在垂直河岸方向上的分速度v_⊥=vsinα，则船渡河所用时间为

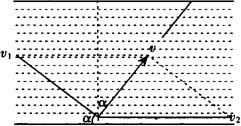
图1

由①式可知，当sinα=1即α=90°时，v_⊥最大，t最小，此时船身垂直于河岸，航向(船头方向)始终指向正对岸，如图2所示，最短时间为

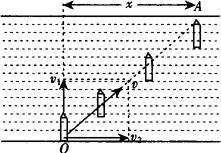
图2

船渡过河时已在正对岸的下游A处，其顺水漂流的位移为

船的实际速度v的大小为

船发生的位移的大小(即线段OA之长)为s=vt_min=5×25m=125m． ⑤

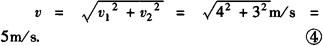
(2)欲使船以最短位移过河，在船速v₁=4m/s，大于水速v₂=3m/s的情况下，可使船头即航向斜向上游一定角度(设与上游河岸夹角θ)，使船的实际速度(合速度v)的方向与河岸垂直指向正对岸，如图3所示，这时船的实际位移大小等于河宽d，位移最短，航程最短，这叫船垂直于河岸渡河，由图可知

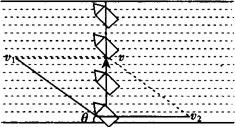
图3

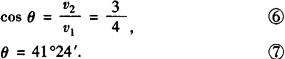
即本题中欲使船以最短位移过河，航向(船头指向)应斜向上游，与上游河岸成角41°24′行驶．

此种情况下，渡河所用时间为

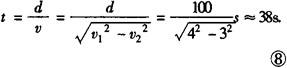
(3)当水流速v₂=5m/s，大于船在静水中速率v₁=4m/s时，船不能垂直河岸渡河了，欲使船渡过河去的航程最短，船的实际速度v的方向与垂直河岸的方向的夹角φ应为最小．如图4所示，以v₂的矢量末端点为圆心，以v₁的大小为半径画个半圆，从v₂的始端O向半圆做切线，则此切线方向就是φ角最小时的方向，即实际速度v的方向(v与v₁、v₂的矢量关系遵守平行四边形定则)，船的实际航程最短，利用直角三角形知识可求得

即当航向(船头指向)斜向上游与上游河岸夹角为37°时，航程最短，其最短航程大小为．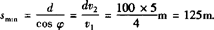

⑾

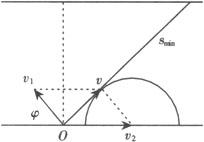
图4

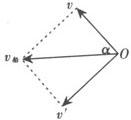
例2 如图所示，用绳子把小船拉向湖的岸边，若收绳的速度v恒定不变，试分析在靠岸过程中，船的速度怎样变化?

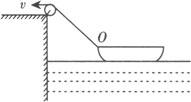
分析 船的实际运动是沿直线水平向左运动，设船速为v_船，则绳与船的连接点O的实际速度也是v_船，它产生了两个效果：一个是O点沿绳子方向的运动，另一个是绕滑轮作顺时针的转动，绳子在O点与水平方向的夹角α逐渐增大，因此，可将O点(船)的运动分解为一个沿绳移动方向的径向运动和一个绕滑轮转动而垂直于绳子方向的切向运动，根据平行四边形定则将v_船沿绳子方向和垂直绳子方向进行分解，如下图所示，在绳子方向的分速度为v，由图可知

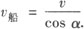
因在船逐渐靠岸的过程中，α逐渐增大，cosα逐渐减小，而v恒定不变，故由上式可知：船速v_船逐渐增大．