博克斯—詹金斯预测法

出处：按学科分类—经济 山东人民出版社《简明经济百科辞典》第883页（1274字）

博克斯和詹金斯提出的一种预测方法。

它根据时间序列资料，从所谓博克斯—詹金斯模型族中寻求和建立一个最佳时间序列关系的预测模型。

博克斯—詹金斯预测法有以下几个重要概念：(1)平稳性序列和自相互函数。平稳性是指时间序列资料不随时间的推移而发生大的波动；自相互函数是研究时间序列x₁，x₂，…，x_t间相邻项相关程度的函数。x_t与x_t+k的自相关函数写成：

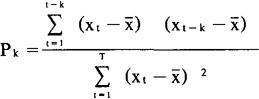
式中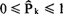，。自相关函数是检验时间序列平稳性的重要手段。当K值增大时，如果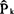_k迅速下降，则说明时间序列平稳，否则是不平稳的。(2)差分。一阶差分定义如下：

△X_t=X_t－X_t－1

二阶差分定义如下：

△²x_t=△(△x_t)=△x_t－△x_t－1

高阶差分(二阶以上)以此类推。

(3)齐次非平稳性序列。这一序列是指经过一次或有限次差分后，可以把不平稳序列变换成平稳序列，(4)博克斯－詹金斯模型分为两个基本平稳模型：①自回归模型BJ(P，0)，数学形式为：

X_t=Φ₁X_t－1+Φ₂X_t－2+…+Φ_pX_t－p+ε_t

式中，Φ_i为方程的参数；x_t为实际观察值；ε_t为随机误差项。②滑动平均模型BJ(0，q)，数学型式为：

x_t=ε_t+Q₁ε_t－1+…+Q_qε_t－q+μ

式中，μ为x_t的平均值，Q_i为参数，ε_t为随机误差项。

由BJ(p，0)和BJ(0，q)出发，可以构成混合回归与滑动平均模型BJ(p，q)，以及处理齐次非平稳时间序列的结合自回归与滑动平均模型BJ(p，d，q)。

BJ(p，q)的基本形式如下：

X_t=φ₁X_t－1+…φ_pX_t－q+ε_t+Q₁ε_t－1

+……+Q_qε_t－q+q

BJ(p，d，q)与BJ(p，q)的形式相同，只是将xi换为△^dx_i，d为差分阶数。

应用博克斯——詹金斯预测的基本步骤是：(1)识别。首先通过P_k检验时间序列x₁，x₂，…，x_t是否平稳，若不平稳则选取适当的d，使差分时间序列平稳。

求出平稳时间序列或差分后平稳时间序列的最佳p，q值，完成模型的识别。(2)估计。用最小平方法或其他方法估计模型的系数，并进行统计检验。若检验通不过，则重新识别模型或另行定式估计，反复数次，直至满意为止。(3)预测。选定模型后，代人前定变量，对未来进行预测。