命令句逻辑
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第75页(1851字)
以逻辑演算为工具研究命令句之间的逻辑关系的哲学逻辑分支。
命令句在现代汉语里又叫祈使句,表示要求、希望或命令别人做什么事或不做什么事。例如,“请打开窗户!”“把书递给我!”“你快走吧!”等等。
命令句里也有逻辑。例如,“请打开这屋子里的所有窗户!这是这屋子里的窗户,所以,打开这扇窗户!”“合上书本!合上笔记本!所以,合上书本并且合上笔记本!”这些推理显然都是正确的。
问题在于有什么办法能判断这些命令句推理的有效性。如果人们能找到一种办法把命令句也能分析为具有真假意义的语句,那么,命令句与陈述句一样,也能在现代逻辑中得到反映。
B·F·切拉斯在这方面做出了有意义的工作。他认为,如果人们把对命令句的分析与产生义务这样一个事实联系起来,那么,命令句总是同一个由它变形而来的将来时态的命题(又叫命令的归结命题或命令的代替)相关的,即命令句的发出总要产生某种义务,而履行这种义务总是在命令句发出以后的一定时期才得以实现的。
例如:“拿酒来!拿烟来!”总是相关于“酒将被拿来,烟将被拿来”这样的命题的。结果,命令句化成了一般的陈述句,变成了普通的命题。不过,这种命题由于带有将要实现的可能时态,决定命令句是否成立就有两个因素:一是发布命令时的状况(句子发出时世界的状态),二是状况间的命令代替关系(即命令的归结命题)。而这两个因素都是与模态逻辑问题相关的。
因此,在模态逻辑的体系上就可以构造一个命令句的逻辑系统。命令句之间的推理关系的正确性便可以在这个系统中得到验证。
下面是Imp命令逻辑形式系统:
一、Imp的形式语言
1.有穷序列的原子命题:P1,P2,…;
2.逻辑符号:~, ,!(义务的命令算子),i(许可的命令算子)。
,!(义务的命令算子),i(许可的命令算子)。
二、Imp的形成规则
1.可数个原子命题P1,P2,……是合式公式;
2.若A是合式公式,则~A、!A、iA是合式公式;
3.若A和B是合式公式,则A B是合式公式;
B是合式公式;
4.只有根据以上三条所形成的符号序列是合式公式。
三、Imp的公理:
(Imp1) !(A B)
B) (iA
(iA !B)
!B)
(Imp2) iA≡~!~A
(Imp3) !A iA
iA
(Imp4) !A !!A
!!A
(Imp5) !A !iA
!iA
四、Imp的推演规则:
(R!)
Imp就是在PC上增加上述公理和推理规则的形式系统。它有如下一些定理:
TH1 !A≡~i~A
TH2 !(A∧B)≡(!A∧!B)
TH3 i(A∨B)≡(iA∨iB)
TH4 (!A∨!
TH5 
TH6 !A≡!!A
TH7 !A≡i!A
TH8 iA≡iiA
TH9 iA≡!iA
TH10 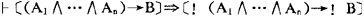
逻辑学家已经尝试构造了为数不少的命令句逻辑系统,但迄今没有一个系统得到公认。