相信逻辑

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第78页（1420字）

属于认识论逻辑的一支，处理含有模态词“相信”的命题之间的逻辑关系。

在相信逻辑中，相信被处理为一个二项关系，一方是相信某种观点的人，另一方是他所相信的论点。假定用x，y，z……表示个别的人，用p，q，r，……表示某种观点，用B表示相信关系，则B(x，p)就表示“x相信p”。

相信逻辑假定了如下一些基本原则：

1．一致性。

1．1 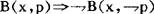若x相信p，则x不相信非p)

1．2 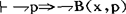(若断定非p，则x不相信p)

相反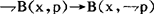，则是不可接受的，因为它的逻辑推论是，在一对互相矛盾的命题中，人们必须相信其中之一，这就排除了取犹疑不决态度的可能。

2．合取的构成和分解。

2．1 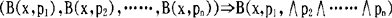(若x相信p₁，x相信p₂，……，x相信p_n，则X相信p₁并且…p₂并且……并且p_n)

2．2 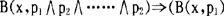、B(x，p₂)，……，B(x，p_n))(若x相信p₁并且p₂并且……并且p_n，则x相信p₁并且p₂并且……并且p_n)

3．极小推理能力。

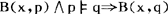
这里“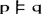”表示q是p的明显的逻辑后承，例如说，以p只需要使用初始的变形规则，通过少于两步(或几步)的推理就可得到q。相反，B(x，p)∧(p→q)→B(x，q)是不可接受的，因为它要求人们必须接受所相信命题的一切逻辑推论，这与日常直觉是相违的。

相反，下述原则即B(x，p)∧B(x，p→q)→(x，q)是可以接受的，它说，若x相信p并且x相信从p可推出q，则x相信q。

上述基本原则使相信逻辑有下述定理：

(1)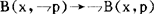(若x相信非p，则x不相信p)

(2)B(x，p)∧B(x，q)→B(x，p∧q)。

(3)B(x，p)→B(x，pvq)(若x相信p，则x相信p或q)。

相反，下述关于重叠的相信的原则是不可接受的：

(4)B(y，B(x，p))→B(x，p)(y≠x)(若y和x是不同的人，且y相信x相信p，则x相信p)。

(5)B(y，B(x，p))→B(y，p)(y≠x)。

但是，下述关于重叠相信的原则是可接受的：

(6)B(x，p)→B(x，B(x，p))(若x相信p，则x相信x相信x相信p)。

(7)B(x，B(x，p))→B(x，p)(这是上一原则的逆)。

相信逻辑还有待于进一步发展、完善。它对于认识论和人工智能研究等有重要意义。