状态空间法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第121页（939字）

在现代控制理论中，用状态方程和输出方程来描述系统的行为和性能的一种基本方法。

是60年代发展起来的一种新方法。被用来研究一些性能指标要求严格的复杂系统，而这些系统可能是多输入多输出的，也可能是时变的(即描述系统的微分方程的系数不是常数，而是时间的函数)。系统本身还可能是非线性的。

在控制系统中，状态随时间变化是有一定规律的。

描述状态变量(即表示系统内部状态的量)随时间变化的规律的方程，称为状态方程。它是输入对状态变量作用的关系式，一般是写成一阶矩阵微分方程的形式。

输出和状态变量的关系式称为输出方程。对于一个n阶连续系统，我们可以用微分方程来表示，其表达式为y⁽ⁿ⁾+a₁y^(n－1)+a₂y^(n－2)+…+a_n－1y+a_ny=u，式中y⁽ⁿ⁾是输出变量y的n阶导数，y^(n－1)是y的n－1阶导数，y是y的一阶导数。

a₁，a₂，…，a_n－1，a_n为常系数。u为系统的输入变量。根据上述微分方程可得出该系统的状态空间表达式的矩阵形式X=AX+Bu，这个一阶微分方程就是该系统的状态方程。而输出方程的矩阵形式则可相应地写成Y=CX。

式中的这些变量一般随时间变化，所以就一般情况而言，u，X，Y都是时间的函数。在上述微分方程所描述的系统中，若已知初始时变量y(0)，及其各阶导数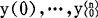已知t≥0时的输入变量u(t)，就完全可以确定系统未来的行为。

根据状态方程和输出方程可画出描述系统的状态变量图，该图可反映系统内部因素与外部输出量之间的关系。

由于现代控制理论是建立在状态变量、状态空间(即在时间t中，状态向量X的一切可能取值所构成之集合，称为状态空间)等概念的基础之上，运用状态方程来描述系统，应用状态空间法来分析系统，所以它就克服了经典控制理论的局限性。它不仅适用于多输入－多输出系统、适用于非线性系统和时变系统，而且还为最佳控制问题的研究带来了方便。在经典控制论中，系统的设计和优化本质上是建立在试探法的基础上的，这与设计人员的经验有很大的关系，因而通常不太容易得到最佳控制系统。

运用现代控制理论和方法，一方面能使工程技术人员依据给定的性能指标设计出最佳控制系统，另一方面还可用更一般的输入代替特殊的输入函数来实现最佳控制系统的设计。