母函数(数论)

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第173页（678字）

也叫发生函数或生成函数。

是数论、组合理论，插值与逼近论中的重要数学工具，设关于函数g(t)在t=0的某邻域内收敛的幂级数为，这就确定了数列｛a_n｝。这时称g(t)为序列｛a_n｝的母函数。

对于函数列｛f_n(X_n)｝，类似地，把在(x，t)空间的某个域内关于x，t收敛的级数K

称为函数列｛f_n(x_n)｝的母函数。例如，二项式系数和勒让德多项式的母函数分别为(1+t)ⁿ和。

若已知｛a_n｝或｛f_n(x)｝的母函数，就可以给出a_n和f_n(x)的积分表示。例如，对后一种情形，有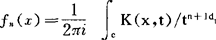，其中积分路径C是以原点为中心，正方向的充分小的圆周，可以把母函数关于t解析开拓到幂级数的收敛域以外。

由于许多重要的正交函数系的简单母函数是已知的，因而借助于母函数，可以导出数列和函数列的许多重要的解析性质。所以，母函数的方法在数学，计算数学与工程力学中被广泛地应用。

当参数不是整数n而是连续变量的情形，则可将母函数作为拉普拉斯变换或富里埃变换的形式来定义。

最早将母函数方法应用到数论的广泛领域中去的是欧拉，他首先巧妙而简捷地解决了线性丢番图方程的解数问题。例如，设n为一正整数，若线性丢番图方程x+2y+5z+10u+20v+50w=n的非负整数解的个数为An，根据幂级数的乘法可知，A_n的母函数就是：

并且乘积级数中Sn的系数就是A_n，因此由泰勒展开定理得，这便是关于A_n的一般公式。