传热过程的分析方法

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第195页（853字）

传热过程既有平衡态又有非平衡态的问题，热量传递的三种基本方式是导热、对流及辐射，下面分别描述它们的分析方法。

(1)热传导。有导热介质，没有质量交换，但由于温度差引起的能量输运过程。

一维导热方程——付里叶(Fourier)公式

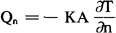
式中Q_n是法线方向单位时间内的热流量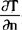，是垂直于面积A的方向上的温度变化率，称作“温度梯度”，K是导热系数(它与导热物质的材料有关)，负号表示热量沿着温度降低方向流动。

三维导热方程为

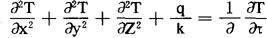
式中导温系数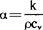，(ρ为材料密度，C_v为定容比热容)q为单位时间单位面积内传递的热量。

(2)对流传热。有导热介质及质量交换的输运过程。

其数学分析较复杂，往往与流体力学的数学形式相联系，分别需要建立系统的质量守恒(流体连续方程)，动量守恒(需要考虑粘滞性、压力以及体膨胀等问题)以及能量守恒(包括热传导)三种微分方程，然后由边界条件对三项守恒方程式求解。这里只介绍固体表面与环境流体间对流传热方程(又称牛顿冷却公式)为

Q=hA(T_s－T_∞)

式中Q是单位时间由单位表面积传递到环境流体的热量，h是对流换热系数，(它是与系统几何条件、流体的物体及流动情况有关的量)A是表面积，Ts是表面温度，T_∞是环境温度。

(3)辐射传热。

没有导热介质，是电磁波(波长范围在10⁷～10²米间)辐射。

由辐射中斯芯藩－玻尔兹曼定律指出黑体在任何温度T时辐射率为

e(T)=σT⁴

式中σ称为斯芯藩－玻尔兹曼常数，它是与物质无关的普适常数σ=5．67032×10^－8瓦特·米^－2，K^－4，得到单位时间内辐射传递的热量为

Q=Aασ(Tw²－T²)

式中α为温度T时的吸收率(黑度)，A为辐射体面积，Tw为接受辐射物体的温度。