最小平方(预测)方法
出处:按学科分类—自然科学总论 山东人民出版社《方法大辞典》第453页(1082字)
指使倾向性的回归直线到实际资料各点之间的距离最小,即偏差平方和最小,这条直线最能代表实际资料变动的特点,因而也最适宜作为预测的标准。
这种方法称为最小平方(预测)方法。
在趋势线为直线y=a+bx的情况下,用偏微分可得出两个标准方程式如下:
∑y=Na+bx
∑xy=a∑x+b∑x2
根据标准方程式,可求出a和b,然后根据a和b决定直线方程式。
除直线趋势线外,常用的非直线趋势线至少有下列6种:
(1)二次抛物线y=a+bx+cx2
(2)三次抛物线y=a+bx+cx2+dx3
(3)简单指数曲线y=abx
(4)修正指数曲线y=a+bcx
(5)计算艺术曲线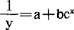
(6)冈珀茨曲线y=a bex
运用最小平方方法应注意几个问题:
(1)选择一种最适合的趋势线,有时不仅是决定哪一种形式的方程式的问题。如果当被预测的变数在整个时间过程中发生了根本的变化,那么,最好将时间数列在变化前和变化后这两个阶段分开,分别配合一条趋势线,这样可能更符合实际情况,而用外推方法进行预测也会取得更好的效果。
(2)某些趋势线方程式,如二次和三次抛物线及指数曲线的y值可以无限地上升或下降,这会使预测失去意义。因此,这种曲线只能在某一时间范围内有意义,作过于远期预测是不适宜的。
(3)抛物线的使用一般只限于二次或三次抛物线,四次或更高次抛物线比较少用。因为从表面上看,由于用了更多的常数,似乎对时间数列配合得更好了,但这样却受随机变动的影响越来越大,反而不能正确反映趋势,因而使预测结果的意义也随之而减少。
(4)上面4~6种曲线,一般称为增长曲线。从长远看,许多数列都经过三个发展阶段:即缓慢发展阶段,迅速扩张阶段,成熟减速阶段。
三个阶段形成了S形曲线。