表意符号——一种按算术语言构成的纯思维的符号语言

出处：按学科分类—自然科学总论 山东人民出版社《方法大辞典》第772页（1083字）

逻辑学家弗雷格的第一部着作。

发表于1879年。

在此书中，弗雷格主要考虑的是构造一种纯思维的形式化语言，即比普通语言更加规则的、并能更好地适合于保证推演精确性的符号系统，以便使逻辑摆脱日常语言的含混不清以及主观心理因素的渗入。例如，他用一条垂直短线加上一条水平短线表示右方的记号或记号组合(代表命题)是被断定的；垂直短线“1”称为判断短线，水平短线“——”称为内容短线。

把连结两条水平短线的垂直短线称为条件短线。

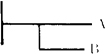
分别表示1－B→A和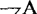。他还引入了许多其他的符号，分别表示同一、函项和变目、量词等等。

在上述符号语言的基础上，弗雷格第一次构造了一个公理化的一阶函项演算系统(即一阶谓词演算)，它包括下述九条公理(改用现今通行的符号表述)：

1．p→(q→p)

2．(p→(q→r))→((p→q)→(p→r))

3．(p→(q→r))→(q→(p→r))

4．

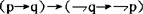
5．

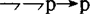
6．

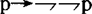
7．(x=y)→(F(x)→F(y))

8．x=x

9．

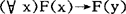
除此之外，弗雷格还明确陈述或实际使用了一些推理规则，它们是分离规则、代入规则、后体概括规则、后体限制规则。

以上9条公理和四条推理规则就构成了一阶谓词逻辑的公理系统，严格地说，是带等词的一阶谓词逻辑公理系统；其中前六条公理加上分离规则、代入规则，就构成了命题逻辑的公理系统。

可以证明，弗雷格的系统满足一致性，完全性，但不满足独立性。

但是，这部书在逻辑上并没有发生实际的影响，因为哲学家害怕其中的那些符号和符号系统，而数学家又害怕那些哲理性的讨论。直到罗素大力推举之后，此书及弗雷格的其他着作才受到人们的广泛重视。