单纯形表

出处：按学科分类—经济 中国财政经济出版社《中国物资管理辞典》第494页（2007字）

单纯形解法的表格化。

每反复迭代一次，连续编制一张，表达在当前解时由基底变量达成的基底可行解及其目标函数值，同时反映约束方程组各变量在迭代运算中的交换结果和检验数。单纯形表的一般格式(以初始表为例)如下表所示：

表中，顶行c_j填入各变量在目标函数中的系数；最下面两行，一行是z(或z_j)行表示在达成的基底可行解条件下的目标函数值与单位损失；另一行，(c_j－z_j)行为检验数。单纯形表分为三部分：第一部分由c_B、x_B及b列组成。x_B列填入基底变量，c_B列填入各该基底变量的目标函数系数，b列填入各该基底变量的解答值。

第二部分由决策变量x₁，x₂，…，x_n和辅助变量x_n+1，x_n+2，…，x_n+m各列及其在约束方程中的相应系数a_ij(i=1，2，…m；j=1，2，…n)组成。这些系数反映了“列”与“行”变量之间的置换比例，其数值随着每次运算不断变换。第三部分由检验比θ_j列组成。

现说明单纯形表的编制和计算步骤如下：(1)编制初始单纯形表，确定初始基底可行解。

首先引入必要的辅助变量(松弛变量，剩余变量、人工变量)，使约束方程不等式化为等式，并使之变换成为适合于进行单纯形解法计算的规范形式。然后根据约束方程组和目标函数方程的各项参数构成第一张单纯形表。

为确定初始解(如求目标函数的极大值)，一般使决策变量x₁，x₂，…，x_n等于零，而松弛变量x_n+1，x_n+2，…，x_n+m就解得一组非负值等于b₁，b₂，…，b_m进入“基底”，达成一个可行解，其目标函数值为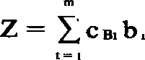：。这就相当于在图解法中以原点作为迭代的始点。

以上进入基底的变量称为“非零变量”或“基底变量”，而由基底变量达成的可行解称为“基底可行解”。取值为零而未进入基底的变量称为“零变量”或“非基底变量”。(2)计算各列变量的“单位损失”Z_j和检验数C_j－Z_j，以确定“调入列”和“调入变量”。所谓“单位损失”，指如将该列非基底变量调入“基底”一个单位，将使目标函数值相应减少的收益额，其计算公式如下：

j=1，2，…，n)

该非基底变量每一单位能提供的收益为C_j，减去其“单位损失”Z_j，所得非负差额c_j－z_j就是该非基底变量调入基底能使目标函数值增加的净收益。

C_j－Z_j称为检验数(或判别数)，用来检验是否已求得最优解，和判别调入的非基底变量能否最大限度改进现在的基底可行解。对于求极大(或极小)值的线性规划问题，选择检验数为最大正值(或最大负值)的所在列作为调入列，称为主元列，在表中该列的下方用“^{标出，相应变量即为调入变量；有时，可能遇到相同的两个或多个检验数，一般可任选其中一个作为调入列和调入变量。当全部检验数已取得非正数(或非负数)，不能使现有目标函数值再有增加(或减少)，说明已求得最优解，这时就说该问题达到最优状况。(3)计算检验比，以确定“调出行”和“调出变量”。}

检验比是用以选择调出行和调出变量的一种数字特征。在单纯形表中以θ表示，各行的检验比计算依公式：，其中，K为调入列，a↓（iK为该列第i行的约束方程的系数，并要求a_iK＞0(如为零或负值，可舍去不计。但如K列中的a_iK都为零或负值，则问题无解)，b_i为同一行的基底变量的解答值。为了保证置换的可行性，应取检验比中的最小者。

当时，即选择第L行为调出行，称为主元行，在表中该行的右端用“→”表示，其所在行的基底变量即为调出变量，在新编的单纯形表中，它离开基底被调入变量所置换，而θ_L的数值即为调入变量在新编单纯形表中的解答值，有时，在选择调出行时，可能遇到相同的二个检验比，一般可任选其中的一个。但应注意避免由于选择不当，置换后在新的基底变量中出现有零值，产生退化的解。(4)以“旋转元素”为中心，进行旋转运算，编制新的单纯形表。

在原来的单纯形表中，上述主元列和主元行相交叉处的调入变量的系数称为“旋转元素”或“旋转元”，记作a_LK，以圆圈圈起，以便于辨认。

所谓旋转运算，就是将一个调入变量，以旋转元素为中心，进行行与列的变换，把给出的一组约束方程变换为另一组等价的约束方程。旋转运算的步骤是：①将调入变量置换基底中的调出变量，并将旋转元素a_LK除以旧表中调出行(L)各元素a_Lj和b_L，得出新表调入行的新元素和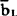填入新表，计算公式为：

②计算新表中其它各行的新元素，填入新表，计算公式如下：

新表其它各行新元素＝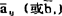

通过以上旋转运算，在新表的基底变量列形成一个单位矩阵，它的对角线各元素为1，而其它各元素为0。

(5)以新的单纯形表为起点，反复进行第二、三、四、五步骤，直至求得最优解为止。