F－分布

出处：按学科分类—社会科学总论 上海人民出版社《统计辞典》第737页（537字）

为美国统计学家斯纳德柯(G．W．Snedecor)所推导。

其主要作用是检验方差的同一性。设X，为独立随机变量，分别服从自由度为m及n的X²分布。则随机变量具有下列密度函数：

其中：Γ指伽玛函数，称此随机变量服从F分布，或称自由度为(m，n)的F随机变量，记作F(m，n)，F－分布的图象为单峰，当m固定时，n愈大则愈接近对称，n愈小则右尾愈长。它的数学期望=n/n－2，(n＞2)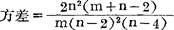；，(n＞4)。F－分布有一个重要性质：如果x～F(m，n)，则，这一性质在F检验的计算中很有用。

两个独立N(0，1)的样本估计方差的比值，

它是F检验法的理论依据；F值表也是根据这个分布密度来编订的。

p〔F(m，n)＞F_m，n，a〕=a

式中F_m，n，a为上侧分位数。

F－分布经常用于方差分析，回归分析，两正态总体方差对比检验，二项分布的统计估计和统计检验等。

因此，它是统计中的重要分布之一。