动态规划

出处：按学科分类—经济 经济科学出版社《企业管理学大辞典》第554页（1113字）

求解多阶段序贯决策问题的最优化方法。

多阶段序贯决策问题是一种复杂的决策问题，它在时间(或是由解题方便而规定的其他因素)上分为若干阶段，其中每阶段都需做出决策，而困难之处在于前面做出的决策将会影响后面的决策。求解一个动态规划问题，所遵循的方法来自于“最优性原理”，即一系列的决策如果是最优的话，那么它其中任何一个子决策(若干相连的决策)也是最优的。

这从直观上来说是明显的，因为如果子决策不是最优的话，将可以找到一个更好的子决策，这将使得总的一系列决策更好，从这条原理可以得出动态规划问题的求解方法，由后向前，逐步递推。为了讲述解法，先引进一些记号：设阶段变量k(1≤k≤n)表示决策阶段；状态变量S_k表示第k阶段的状态，这由初始状态及已作出的决策而定；决策变量x_k(S_k)表示在第k阶段时处于S_k状态下所做的决策；损益变量d[S_k，X_k(S_k)]表示在S_k状态下作决策x_k(S_k)所带来的损益；f_k(S_k)处于S_k状态下的最优决策序列。有了这些变量，根据最优性原理，动态规划的模型可以表达为：

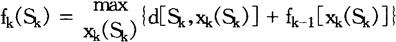
这表示第K阶段的最优决策序列是由前一阶段(注：一般标号以最靠近目标的标为1阶段，稍远的标为第2阶段，以此类推)所做的最优决策序列与本阶段所做决策的损益之和的最大值。

例：最短路问题，已知A地到D地的各条道路及长度如图11－6，求从A到D如何走最近。

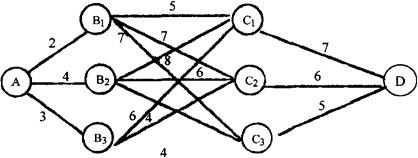
图11－6

在这个问题中，阶段明显为A→B→C→D三个阶段，各C是第1阶段，各B是第2阶段，A为第三阶段，状态变量即各地点，决策变量即各道路，损益变量即各道路之长，最终的决策序列即一系列道路，而目标为路长之和最短，求解如下：

从图中直接可以看出：

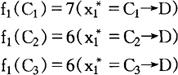
(注：变量加星号表示最优解)

对于B₁：

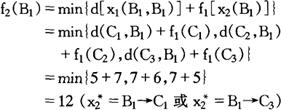
同理可求得B₂，B₃：

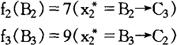
对于A：

因此，最短路长为11，走法为(将各最优解串联即可)，A→B₂→C₃→D。