穆迪次序图分析法

出处：按学科分类—经济 经济科学出版社《企业管理学大辞典》第587页（1083字）

对方案的优劣进行两两对比以确定全部方案的优劣次序的决策方法。

由穆迪(H．Moody)所发明。次序图有好几种类型，这里介绍两种：

(1)简单次序图

图11－19表示A，B，C，D四个方案(或要素、员工绩效、产品好坏等等)相比较之结果，纵列表示比较方案，横行表示被比较方案，当比较方案优于被比较方案时，在交叉处填1，反之则填0，由于自身不与自身相比较，故对角线上不填数。如A优于B，则在第一行第二列填1，同时在第二行第一列填0。将横行各数相加即是各方案的合计得分，分数值越大方案就越好，当有的方案得分一样时，则应比较分值相同的各方案之间对比的结果，如A，B同得2分，则比较A，B之间的关系。从图11－19中可以发现A优于B，故在A的数值2的上面加一“+”，以示区别，最终各方案总的顺序(从优到劣)为：A、B、D、C。

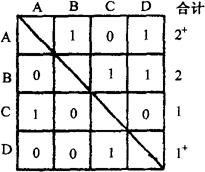
图11－19

(2)多输入加权次序图。由于在简单次序图中只表示了方案间有优劣，但未描述出优劣的大小，为了弥补这个缺陷，就有了多输入加权次序图(见图11－20)，这种图的结构与简单次序图的不同之处在于表格中填的数字不再是0或1，而是0到m间的一个数，具体的决定方式有两种：一种是集体投票。由m个评委参加评判，假如在A与B的比较中有k₁(0≤k₁≤m)个评委认为A优于B，则应在第1行第2列填k₁；若有k₂(0≤k₂≤m，0≤k₁+k₂≤m)个评委认为B优于A，则应在第2行第1列填k₂。注意这里有评委弃权的可能性，因此k₁+k₂可能小于m(即投A票的与投B票的评委总数少于应投票的评委总数)。当有两个以上方案得分相等时，确定优先顺序的方法同上，但这时有可能出现两方案无法区分优劣的情形，举例如图11－20，m=5。此例中，B、C方案得分相等，而评委在对B、C之间的优劣进行表决时，各投1票给B、C，因此B和C无法分辨其优劣。若要避免这种情况，只有限定评委不许弃权且评委的人数为奇数。

另一种是表示优劣相差程度。这时m代表两两相比时双方得分的总和，即把m分配给双方，双方得分相差越大则表明优劣程度相差越大。

如m=10，比较A与B时，分别给A，B各5分，则表示A与B相等，给A4分，给B6分，则表示A比B略差，给A9分，给B1分，则表示A比B好很多。其他的步骤与简单次序图相同，以合计分值表示优劣，分数越高方案越好。