最优契约

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第118页（937字）

在存在隐蔽信息或信息不对称情况下，委托－代理问题中就存在如何订立激励合约的问题。

假定委托人不能观测到代理人的行动选择和外生变量，只能观测到产出。此时，代理人的激励相容约束是起作用的，因为不论委托人如何奖惩代理人，代理人总是会选择最大化自己效用水平的行动。换言之，委托人不可能使用"强制合同"来迫使代理人选择委托人希望的行动，而只能通过激励合同诱使代理人选择委托人希望的行动。委托人的问题是选择满足代理人参与约束和激励相容约束的激励合同以最大化自己的期望效用函数，满足这样要求的合约就称为最优契约。

例如，在股东雇佣经理的问题中，假设经理可以选择的行动为L和H，L代表低努力水平，H代表高努力水平。记f_H(π)是经理付出高努力后利润的分布密度，f_L(π)是经理付出低努力后利润的分布密度，两个分布函数都是委托人和代理人的共同知识。

委托人要设计一份雇佣合同w(π)(根据事后的利润决定报酬)，这份合同既可以使得经理努力工作(经理选择H)，又可以使得股东最大化他的净利润的期望效用。委托人选择激励合同w(π)，在满足个人理性约束和激励相容约束的条件下最大化经理努力工作时委托人净利润的期望效用：

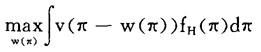
满足约束：

∫u(w(π))f_H(π)dπ－c(H)≥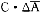

∫u(w(π))f_H(π)dπ－c(H)≥∫u(w(π))f_L(π)dπ－c(L)

令λ和μ分别代表个人理性约束和激励相容约束的拉格朗日乘子，上述最优化问题的一阶条件为：

这个条件被称为莫里斯－霍姆斯特姆(Mirrlees-Holmstrom)条件。

μ=0条件转变成对称信息条件下可以导出的帕累托最优风险分担合同，但是在非对称信息条件下μ＞0，表明在非对称信息的条件下存在激励与保险的替代。