罗伊恒等式

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第214页（313字）

在消费者理论中，设价格p=(p₁，…，p_n)，收入为w。

当间接效用函数v(p，w)是可微时，对p=(p₁，…，p_n)＞0和w＞0，有

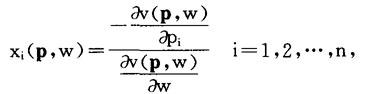
其中x_i(p，w)是在价格p和收入w之下消费者对第i种商品的需求函数，称为罗伊恒等式。例如设效用函数u(x₁，x₂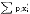)=x+x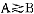，可求出间接效用函数v(p₁，p₂，w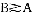)=(p+p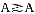)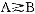^－w，其中r=ρ／(1－ρ)。

由罗伊恒等式，对商品1的需求函数

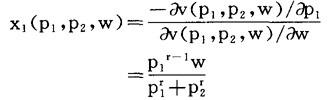
类似地得x₂(p₁，p₂，w)=p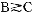^－1w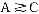／(p+p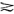)。