阿罗－德布鲁一般均衡模型

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第225页（1533字）

瓦尔拉斯最先建立一般均衡理论，在研究均衡解的存在性时，他仅从方程的个数和未知数的个数一样多，就认为均衡解一定存在，这从数学上看是不严格的。

直到20世纪40年代作为布劳维尔(Brouwer)不动点定理的推广--角谷不动点定理出现后，在50年代由阿罗、德布鲁等应用集合论方法重建一般均衡模型才给出均衡解存在性的严格证明。阿罗－德布鲁一般均衡模型是一种竞争均衡，其含义如下：

设一经济由Ⅰ个消费单位、m个生产单位组成，生产、消费、交换n种财货(包括生产要素和产品)。对生产和消费单位分别作如下假设：

1．第k个生产单位有一个生产过程的集合(生产可能性集合)Y_k，k=1，…，m，它满足

(1)Y_k是包含原点0在内的闭凸集。

(2)Y_k∩R={0}，其中Y=Y_k，这意味着在生产中没有投入就不会有产出。

(3)Y∩(－Y)={0}，这意味着生产过程具有不可逆性。

2．第i个消费单位有一个消费(可能性)集合Z_i和一个效用函数u_i(x)，i=1，…，I，它们满足

(1)Z_i=b_i+R，即Z_i是由非负卦限平移到b₁而成，其中b_i是第i个消费单位的起码生活水平。

(2)u_i(x)是连续的、拟凹的和严格单调的。

3．对每一个i和k，存在常数θ_ik≥0，且#θ_ik=1。

当第k个生产单位获得利润π_k时，第i个消费单位就分别利润θ_ikπ_k。

4．第i个消费单位在开始时拥有第j种财货a_ij单位，记a_i=(a_i1，…，a_in)，称a_i为第i个消费单位的初始财货。

5．存在一个生产过程_k∈Y_k，(k=1，…，m)，使得

这意味着此经济有可能生产出这么多的产品，使得这些产品和初始财货加起来能超过起码的总消费水平。

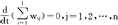一个向量组{；₁，…，₁；₁，…，#_m)如满足下列三个条件，则称它为竞争均衡：

1．生产单位的利润最大，即对第k个生产单位，应有

π_k()=_k ·y=·(k=1，…，m)

2．消费单位的效用最大，即对第i个消费单位，应有

u_i(x_i)=maxu_i(x) (i=1，…，I)

x∈{x∈Z_i|·x≦a_i+θ_ikπ_k()}

3．需求和供给的平衡，即：

(有时，条件3由下述条件3′代替

3′．总需求不超过总供给，即

则在假设1至5之下，存在满足条件1至3的竞争均衡。