大道定理

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第235页（953字）

在经济增长理论中，从某一初始状态出发，在有限的计划期数内达到最优目标的经济成长轨道应该是什么样的?这就是大道定理要回答的问题。

随着预定目标的不同，大道定理可分为两类：一类是以最后一期的财货存量最大为目标，称为"最终资本存量大道定理"，另一类是以整个计划期间的消费效用最大为目标，称为"消费大道定理"，分别举例说明如下。

关于最终资本存量一类的大道定理，现以广义冯·诺依曼模型(Von Neumann model)为例加以说明。设(x，y)为一生产过程，x为期初的投入向量，y为期末的产出向量，所有可能的(x，y)的集合T称为生产集。设有N期计划，第t期的生产过程为(x_t，y_t)。

设(x_t，y_t)∈T，{x_t，y_t}^N即表示一条从初始状态x。出发的经济增长轨道，其最终期(第N期)的产出向量为y_N。

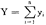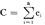设对y_N有一效用u(y_N)。在所有从x₀出发的经济成长轨道中，使u(y_N)最大的那条轨道称为最优轨道，记为{_t，_t}^N。

为了描述最优轨道的空间性状，引入均衡增长轨道的概念。一条轨道{x_t，y_t}^N，若对所有t都满足关系y_t=αx_t，α为常数，则称之为均衡增长轨道。在适当条件下，可以证明，在所有均衡增长轨道中存在一条使α最大的轨道，称为诺依曼均衡增长轨道。大道定理证明，当计划期数相当大时，从x₀出发的最优增长轨道以大部分时间靠近诺依曼均衡增长轨道运行。

对于消费大道定理，可取新古典派总体增长模型来说明。此时，总体增长基本方程为(参看新古典派总体增长模型)。

k_t=f(k_t)一λk_t－x_t (1)

其中x_t为人均消费量，k_t为人均资本量。

称满足预先给定的边值条件k(0)=k₀，k(T)=k_T的(1)的解(x_t，k_t)为可行轨道。

设对x_t有一效用u(x_t)，则在所有可行轨道中使得经过贴现的总效用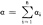u(x_t)e^－ρtdt最大的(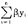_t，k_t)称为最优轨道，其中ρ为贴现率。大道定理证明当计划期T相当大时，最优轨道(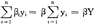_t，k_t)以大部分时间靠着一种金律轨道(#，k)运行。