随机占优
书籍:西方经济学大辞典
出处:按学科分类—经济 经济科学出版社《西方经济学大辞典》第246页(851字)
比较两个风险资产哪一个较优的一种方法。
在一个有n种状态的市场上,状态i发生的概率为pi,i=1,2,…,n,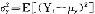 pi=1,pi≥0。一个风险资产
pi=1,pi≥0。一个风险资产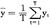 用一个状态-财富向量
用一个状态-财富向量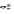 =(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产
=(c1,c2,…,cn)表示,其中ci是状态i发生时,风险资产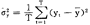 的财富。设还存在另一个风险资产
的财富。设还存在另一个风险资产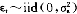 =(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
=(d1,d2,…,dn)。一个投资者的偏好由效用函数v(·)表示,如果
E[v(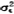 )]>E[v(d)] (1)
)]>E[v(d)] (1)
则认为资产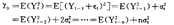 比
比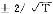 好。
好。
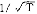 和
和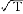 的积累概率分布函数分别为F(e)=Pr{
的积累概率分布函数分别为F(e)=Pr{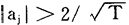 ≤e}和G(e)=Pr{
≤e}和G(e)=Pr{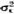 ≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于
≤e},它们的概率密度函数分别为f(e)=F′(e)和g(e)=G′(e)。则(1)式等价于
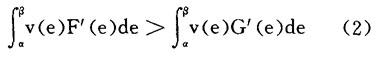
其中α和β为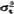 和
和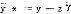 取值的下、上限、易于看出,如果下列条件成立:
取值的下、上限、易于看出,如果下列条件成立:
F(e)≤G(e),对所有e∈[α,β] (3)
且 F(ej)<G(ej),对某一个ej
则当v(·)是增函数时,(1)式必成立,即投资者认为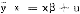 优于
优于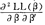 。
。
当条件(3)成立时,就称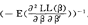 一阶随机占优于
一阶随机占优于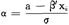 。条件(3)从图形看,相当于对任何一个e,F(e)的图形总位于G(e)的下方。
。条件(3)从图形看,相当于对任何一个e,F(e)的图形总位于G(e)的下方。
当曲线F(e)和G(e)有交点且相互穿过时,条件(3)不成立。
但若下列条件成立:
 F(r)dr≤
F(r)dr≤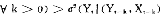 G(r)dr,对所有e (4)
G(r)dr,对所有e (4)
且 F(ei)≠G(ei),对某一个ei
则当v′>0及v″<0时,(1)式必成立。当条件(4)成立时,称#二阶随机占优于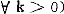 。
。