连锁型加权指数

出处：按学科分类—经济 经济科学出版社《西方经济学大辞典》第851页（1399字）

编制综合物量指数和综合价格指数遇到的最棘手问题是选择权数和权数基期。

例如，编制综合物量指数，一般采用商品和劳务的价格作为权数。因为商品和劳务的相对价格经常变化，使用不同时期的相对价格作为权数，计算得的物量指数会出现不同数值。这里就发生权数基期问题，若是采用固定基期权数，编制的指数往往出现下述情况：固定基期年份以后指数数值较实际变动偏高；而固定基期年份以前的指数数值则较实际变动偏低，即统计学所称的"权数偏误"(weight bias)。

经济统计学者很早就注意研究如何消除权数偏误。费雪(I．Fisher)提出将拉氏公式指数和帕氏公式指数进行几何平均，即所谓理想公式指数。以后，狄维西亚(F．Divisia)、托恩奎斯特(L．Tornquist)曾创立各自的指数公式。

近年来，经过迪沃特(W．Erwin Diewert)、霍尔顿(Charles R．Hulten)等学者深入研究，采用连锁型加权指数可以避免权数偏误。

以实际国内生产总值(GDP)为例，连锁型加权物量指数的计算程序和方法如下：

设Q_t－1，Q_t，Q_t+1，Q_t+2…Q_t+n为商品或劳务在t－1，t，t+1，t+2，…t+n各时期的数量；

P_t－1，P_t，P_t+1，P_t+2…P_t+n为该商品或劳务在t－1，t，t+1，t+2…t+n各时期的相应价格。

第一步，分别计算从t－1到t的拉氏和帕氏综合物量指数：

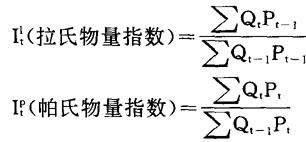
按费雪公式计算从t－1到t的综合物量指数：

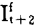(费雪物量指数)

用同样方法计算从t₁到t+1的，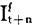

从t+1到t+2的，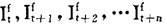

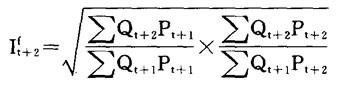
一直计算到#。

第二步，将算得的各时期的费雪指数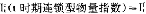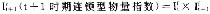依次连乘联结(chained)，所得数值即为连锁型物量指数，如下所示：#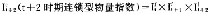

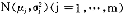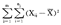
余可类推。

从上述计算程序和方法可见，连锁型物量指数考虑到各时期内相对价格的变化，因而不会发生权数偏误，能够较准确地反映实际GDP的变动趋势。

编制连锁型价格指数的程序和方法与编制物量指数类似。

就编制连锁型GDP价格指数而言，只要把公式中的Q和P换位即可。

当前西方国家统计机构编制综合经济指数，有些已废止固定权数指数，采用连锁型加权指数(如法国和美国)；有些兼用固定权数指数和连锁型加权指数(如荷兰和挪威)。