方程

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第141页（606字）

含有未知量的等式。

由多项式所组成的方程叫代数方程；未知量是对数函数、指数函数、三角函数、反三角函数等方程称为超越方程；未知量是函数的导数的方程称作微分方程。此外，还有积分方程，泛函方程，算子方程等。

使等式成立的未知量的值称为方程的“根”或“解”，对未知量的任何值，总成立的等式称为“恒等式”，求方程的根称为“解方程”。设f(x)为关于x的多项式，则f(x)=0即为代数方程。方程f(x)=0表达形式是一个矛盾的统一体。从形式上看该统一体处于平衡状态，但这种平衡是相对的、有条件的。

首先，只有某些个别的x值能使其处于平衡状态，而对于整个复数系统而言统一是不平衡的。方程与恒等式是对立统一的。

其次，方程的平衡是相对的有条件的包含两层辩证关系。

其一，当方程中的系数暂时固定时，方程的根是其平衡的条件；其二，上述的平衡也孕育着不平衡，一旦方程中的系数变化时，平衡便被破坏。方程的不平衡是绝对的，无条件的。解方程就是寻找平衡的条件。

例如，一元二次方程x2+px+q=0，求根公式为：

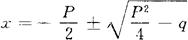
首先，当方程中系数p、q满足上述关系时，方程处于平衡状态；另方面，当方程中的系数变化时，上述x值又不能使方程平衡。因此，对暂时固定的p、q所得二次方程的根使方程所处的平衡状态也是相对的、有条件的，一但p、q中有一值变化，平衡状态便被破坏。