极限方法

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第380页（535字）

亦称“无穷小法”。

数学中的一种重要方法。其基本思想是：为了确定某常量a，最先加以确定的是一连串愈来愈准确的近似值，而数列a₁，a₂，…a_n，…在对这一连串近似值的考察中，即从这近似过程本身的考察中，把常量a的准确值唯一地确定下来。

其过程描述如下：数列a₁，a₂…a_n…若当n无限增大时，数列的一般项a_n最后无限制地趋于常量a，则称被确定的常量a为数列{a_n}的极限；或说数列收敛于a，记作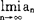=aa极限方法的实质是用无限表示有限，用近似的量表示精确的量。

通过这种实质上是深刻的辩证方法认识到稳定不变的事物是整个过程、运动的必然结果。自然界处在不停的运动、变化过程中，是与时间、空间密不可分的，而这种运动、变化的过程是无限的，为了在这无限的过程中准确地反映、揭示自然界中量的关系，自然应当选用极限方法。它的创立是对于那些不能用算术、代数以及初等几何的简单方法求解的问题顽强探索的结果。它深刻、准确地揭示了自然界中复杂量关系的实质，是辩证法在数学中应用的结果。微积分学中一些重要概念，如微商、积分、收敛级数的和等都是用极限思想建立的。极限方法的创立使近代自然科学得以蓬勃发展。

它与数学中形而上学方法相对立，究其实质是辩证的方法。