波函数

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第552页（505字）

量子力学中用以描述波粒二象性运动状态的函数。

是一个时空多元复变函数。在量子力学理论中有重要的作用，至今实验上还不能直接测定。它遵守薛定谔方程。

量子力学的状态用波函数描写，被称为量子力学第一原理或波函数原理。

量子力学的第一个波函数是根据德布罗意假设建立的平面波函数φ(r，t)=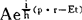是描述自由粒子波粒二象性运动状态的。常数A表示等幅波动。

满足薛定谔方程的波函数，一般都是束缚粒子的波粒二象运动状态，因此波函数的振幅都是调制的，不是常数。当束缚势不随时间变化的情况下，满足薛定谔方程的波函数具有定态形式

φ(r，t)=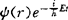

振幅φ(F′)只跟坐标有关，满足一个能量的本征方程，也称定态薛定谔方程式为振幅薛定谔方程。对于除能量外的其他力学量，波函数一般满足一个本征方程称本征波函数或本征态，本征态和它所对应的本征值是一一对应的。力学量的取值特征由本征值表示，一般情况是量子化的。波函数模量的平方表示粒子出现在空间体积元的几率，实验可以测量W=∫|φ(r，t)|²dr=1，因此波函数在数学上是连续、单值、有限的，按几率归一。