哥德尔不完全性定理

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第695页（966字）

哥德尔1931年发表的一条重要的数理逻辑定理。

它是20世纪最重大的数学成就之一。它指出，任何包含初等数论在内的形式系统中，都有不含自由变元的公式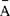，使得A和它的否定式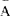都不是定理。形式数论系统的相容性证明不可能在形式数论系统中实现。简单地说，形式系统是形式符号化了的公理系统，它的完全性是指它所包含的每一公式都可判定为是否定理。

而不完全性定理表明，任何包含初等数论的形式系统中，都含有真而不可判定的公式。这就意味着，要把不能不包括初等数论的全部数学纳入一个形式系统中，就必然会出现逻辑上不可判定的语句。

因此，数学的全部形式化是不可能的，把数学完全置于逻辑相容性基础上的努力是无法实现的。哥德尔不完全性定理的出现，在数学发展中产生了深远影响。

它使逻辑主义和形式主义的发展受到挫折，改变了当时数学界单纯追求形式化、公理化的倾向，促进了纯粹数学同应用数学的相互作用。哥德尔在证明不完全性定理的过程中，发展了自然数集上的逆归函数论，对于后来的能行性理论研究有重要推动作用。

哥德尔在证明不完全性定理时使用的配数法，即把形式数论系统中的符号配以自然数，把元数学定理转换为自然数定理的方法，对于数理逻辑研究有重要方法论意义。哥德尔不完全性定理在哲学上也有重要意义。

它表明，数学中的形式系统本身是有局限性的，单纯的逻辑推理不会解决数学中的一切问题，这就从更深的层次上揭示了数学发展同实践的联系。它还表明，数学研究中的能行性思维活动，包括计算机的作用，也是有局限性的，因而必须重视非能行性思维，即辩证的思维在数学研究中的作用。不完全性定理并没有导致不可知论。

它只是从逻辑角度指出形式数论系统中存在不可判定公式，这种公式并非没有真假之分。

不完全性定理的认识论意义在于把“真实性”和“可判定性”这两个相近概念加以区别。两者在逻辑演算中是一致的，而在数学领域中则是不一致的。

数学认识活动的这种特点，为认识论研究提供了新课题，不完全性定理深刻揭示了数学真理的相对性与绝对性的辩证关系，从而证实、丰富和深化了辩证唯物主义真理观。哥德尔用不完全性定理等成果，论证他的新柏拉图主义的数学哲学观点。

现代数学哲学的很多派别对不完全性定理也各有解释。

但不完全性定理本身是数学成果，必须把这一定理同人们对它的各种解释加以区别。