集合论

出处：按学科分类—自然科学总论 天津人民出版社《自然辩证法辞典》第837页（687字）

以集合为基本概念，研究集合的一般运算和性质的数学分支学科。

产生于19世纪末期，主要创始者是德国数学家康托尔。从20世纪初开始蓬勃发展起来，并广泛地应用到数学的各个领域，成为数学最基础的理论之一。

集合可以理解为确定的、不同的对象的总体。

集合中的对象叫作集合的元素。如果对象X为集合A的元素，则称X属于A，记作X∈A，反之则称X不属于A，记做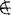xA(或X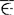A)。集合的基本运算有：并运算、交运算和差运算。设A和B是任意的集合，由A的所有元素和B的所有元素组成的集合叫作A与B的并，记作AUB；由既属于A又属于B的元素组成的集合叫作A与B的交，记作ANB，由属于A而不属于B的元素组成的集合叫作A与B的差，记作A－B。

由有限多个元素组成的集合，称为有限集合。

由无限多个元素组成的集合，称为无限集合。

无限集合是集合论的主要研究对象。

如果集合A的每个元素与集合B的每个元素之间存在某种一一对应关系，那么就说它们有相同的基数或同势。如果可以在集合A的元素与全体自然数组成的集合的元素之间建立一一对应关系，那么就称集合A是可数无限集合；如果可以在集合A的元素与区间[0，1]的全体点之间建立一一对应关系，那么就称集合A具有连续统势。

对于无限集合，可以在整体和部分之间建立起一一对应关系，这就使“整体大于部分”这一法则被破坏了。这表明无限集合与有限集合之间存在着本质上的差异。

无限集合与有限集合之间的质的差异，深刻地体现了辩证法的量变质变规律。