费马大定理

出处：按学科分类—自然科学总论 北京出版社《现代科技综述大辞典上》第32页（5575字）

法国费马(P．de Fermat)大约于1637年在古希腊丢番图(Diophantus)的书《算术》(拉丁文译本)第2卷第8题“将一个平方数分为两个平方数之和”的空白处写下的一个命题。

用今天的语言叙述，费马大定理是：当n＞2时，方程(1)xⁿ+yⁿ=zⁿ没有正整数解。费马当时声称，他已找到一个奇妙的证明。

但是，350多年过去了，不仅没有找到费马的所谓“奇妙的证明”，而且不知有多少优秀数学家试图证明它，均没有成功。所以，费马大定理在今天也叫费马最后定理或费马猜想。

关于费马大定理，从提出到1847年大约过了200年，进展非常缓慢。当n=3，4时，费马本人已给出了证明。100年后，欧拉(L．Euler)发现n=3时费马的证明不完全，因而他给出了一个完全的证明。1823年，71岁高龄的勒让德(A．－M．Legendre)又成功地证明了n=5的情形。

高斯(C．F．Gauss)在给出n=3的情形的另一个证明后，试图证明n=7的情形，但他失败了。为此，高斯称费马大定理是“人们不能证明，也不能否定的命题”。1839年，拉梅(G．Lamé)证明了n=7情形。

第1个对费马大定理作出突破性工作的是德国库默(E．E．Kummer)，他在1847年证明了当n是正规素数时费马大定理成立。

所谓正规素数，是指素数n满足：n不整除分圆域Q(η)的类数，这里η=exp(2πi／n)。库默还给出判断n是不是正规素数的方法：设n＞3是素数，如果n不整除前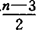个贝努里(Bernoulli)数的分子，则n是正规素数。通过计算，小于100的奇素数中除37，59，67外都是正规素数。但是直到今天，人们也不知道正规素数是有限的还是无限的。

尽管如此，库默由于研究费马大定理而引入的“理想数”的概念，创立了一门崭新的数学分支——理想数论。所以，人们称费马大定理是一只“会下金蛋”的鸡。

这或许是研究费马大定理的一个最重要的理论意义。

1908年，德国佛尔夫斯凯尔(Wolfskehl)逝世前，遗言中要求将10万马克巨款作为奖金授于第1个证明费马大定理的人。

这个奖的设立，大大推动了对费马大定理的研究。

所谓的“证明”纷纷传来，但无一例外均是错误的。

近、现代研究费马大定理，大约可分为3个方面：第1个方面是对一般的n来研究，通常是找费马大定理不成立的必要条件；第2个方面是研究(n，xyz)=1的情形，称为费马大定理的第一情形；第3个方面是研究(n，xyz)＞1的情形，称为费马大定理的第2情形。

对第1个方面，假设方程(1)有正整数解，不妨设0＜x＜y＜z。

1966年，裴利沙斯特利(M．Perisastri)证明x²＞z。1988年，毕尔莱克(K．Bialek)证明x2＞2z+1。1989年，曹珍富证明对2≤m≤n－1均有：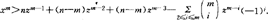

例如取m=2，我们有x²＞nz+n－3。同时，他还证明了xⁿ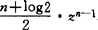＞，以上是关于方程(1)正整数解的估计。关于解的个数方面，英国莫德尔(L．J．Mordell)于1922年提出了一个着名的猜想：在有理数域里，亏格大于或等于2的有理系数二元多项式方程最多只有有限个解。1983年，德国伐尔廷斯(G．Faltings)使用代数几何的深刻工具证明了莫德尔猜想(伐尔廷斯的证明是对于任意数域来证的)，从而推出：当n≥4时，方程(1)如果有(x，y)=1的解，则最多只有有限组。

无疑，这又是对费马大定理的重大突破。利用伐尔廷斯的结果，1985年，希斯－布朗(D．R．Heath-Brown)证明了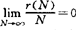，这里r(N)表不超过N使费马大定理不成立的n的个数。这说明，对“几乎所有”的n费马大定理皆成立。此外，当n＜4×10⁶时费马大定理已被证明是成立的。

对第2个方面，即费马大定理的第一情形，早期的结果是热尔曼(S．Germain)与勒让德得到的，他们证明了当n是素数并且2n+1，4n+1，8n+1，10n+1，14n+1，16n+1之一是素数时费马大定理第一情形成立。1894年，文特(Wendt)考虑了由二项式系数()，()，…，()构成的一个循环行列式：

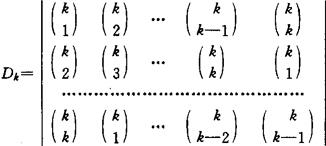
证明：设n是一个素数使得q=2hn+1是素数，如果q⊕D_2h并且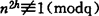，则费马大定理第1情形成立。

由此结果可以推出热尔曼与勒让德的结果。1935年，E．莱默(E．Lehmer)证明：设p是奇素数，则p^p－2·(2^p－1－1)／p整除D_p－1。

卡里兹(Carlitz)沿着这个线索于1960年证明：如果n=p是奇素数，p^p+33①D_p－1，则费马大定理第1情形成立。另一方面，D．E．莱默与E．莱默推广前人结果，证明：设n是素数，如果费马大定理在第1情形时不成立，则对所有素数q≤43均成立(2)q^n－1≡1(mod n²)。

利用这个结果他们证明当n≤25374887时费马大定理第1情形成立。1985年，爱德列曼(L．M．Adleman)与希斯－布朗证明有无穷多个素数n使费马大定理第1情形成立，即有：设S=｛n：n是素数使费马大定理第1情形成立｝，则#｛n∈S：n≤x｝》x^0．6687，符号#｛ ｝表示集合｛ ｝的元素个数。

这个结果也是多年来人们梦寐以求的。1988年，格莱茵维勒(A．Granville)和蒙娜根(M．B．Monagan)将(2)式中的q改进为q≤89，并用此结果证明出费马大定理第1情形对n≤714591416091389成立。

1989年，唐耐(J．W．Tanner)与瓦格斯塔夫(S．S．Wagstaff Jr．)证明当n＜156442236847241729时第1情形成立。

对于n为默森(Mersenne)素数或费马素数的情形，裴利沙斯特利证明费马大定理第1情形成立。1989年，曹珍富证明n为(q^m－1)／(q－1)，(q^m+1)／(q+1)(2①m)或(q^2m+1)／2(q＞2)的素数时，费马大定理第1情形均成立，这里q≤89是素数。

对于n=2p，p为奇素数，1977年特亚尼安(G．Terjanian)利用丢番图方程中的柯召方法证明费马大定理第1情形成立。

利用范迪维尔(H．Vandiver)证明的“若n是素数，n｜xyz且(1)成立，则n³｜ xyz^”的结果，罗特克魏兹(A．Rotkiewicz)、孙琦与曹珍富在1983年前后分别独立地证明8p³｜x或8p³｜y。1987年，曹珍富证明如果方程x^2p+y^2p=z²有整数解，这里p＞3是素数，则4p³｜x或4p³｜y。后来，罗特克魏兹与辛赤尔(A．Schinzel)也得到类似的结果。对于方程x^2p+y²=z^2p，x^2p+y^2p=z^p以及x^2p+y^p=z^2p，曹珍富也证明了一系列定理，这些定理与方程x^2p+y^2p=z²的结论相似。

有趣的是，对方程x^2p+y^2p=z^p的结果，4年后罗特克魏兹才得到。

另一类结果是1953年依恩柯利(K．Inkeri)证明的，即：如果对于素数n方程(1)有满足0＜x＜y＜z，n⊕xyz的整数解，则

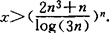
对第3个方面，即费马大定理的第2情形，已有的结果非常少。

原因是前面处理第一情形的方法均不能用来处理相应的第2情形。1929年，范迪维尔继续库默的工作，一般性的证明了：设n是奇素数，如果Q(η)的类数的第2个因子h⁺不被n整除，并且所有贝努里数B_2kn(k=1，2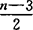，…，)的分子都不被n³整除，则费马大定理成立。

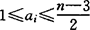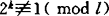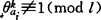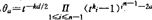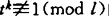但是，因为第2因子h⁺的复杂性，试图避开h⁺就成为摆在人们面前的课题。为此，范迪维尔证明了一系列结果。1954年，D．H．莱默、E．莱默与范迪维尔证明适用于计算的新定理：设n是一个非正规素数，令a_i()是下标使n｜B_2ai，如果对所有的下标a_i，和，则费马大定理成立，这里l是素数，l=kn+1＜n²－n，，t是满足的正整数，。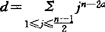

此外，依恩柯利于1953年证明：如果n是奇素数，0＜x＜y＜z，n｜xyz且满足方程(1)，则x＞n^3n－4，。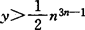

这个结果是可以改进的。

综上所述，费马大定理历史悠久，且在不同时期都有众多数学家参与工作，成为数学界最热门且又是最持久的课题。

目前看来，最重要的结果是从80年代初伐尔廷斯开始得到的。

今后，这一课题的热点将是：(1)使用椭圆曲线来研究。

1986年，费雷(G．Frey)把费马大定理与椭圆曲线联系起来，例如他证明了谷山－魏尔(Taniyama-Weil)猜想蕴涵费马大定理。但谷山－魏尔猜想是算术几何(也称丢番图几何)的深刻课题。在1988年初曾盛传日本宫冈利用椭圆曲线证明了费马大定理，但过后不久，伐尔廷斯便发现了宫冈有一处不可弥补的错误。(2)对abc－猜想的研究。

设a，b，c是互素整数满足a+b+c=0，则对任给ε＞0均有max｛｜a｜，｜b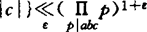｜，。这就是马赛尔(Masser)与奥斯特勒(Oesterlé)提出的所谓的abc－猜想。显然，如果这个猜想被证明，则费马大定理对充分大的指数成立。1988年，赛尔维曼(J．H．Silverman)证明了：如果abc－猜想成立，则有无限多素数n满足。

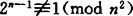(3)关于(1)的解的估计与相关方程的研究。例如当x，y，z中有一个为素数幂时，方程(1)是否有正整数解?对相关的方程如xⁿ+yⁿ=cz^l(n，l均为素数)等，也有过大量的研究，并且将继续吸引人们的注意。(4)初等方法对第一情形将继续发挥作用，例如已知贝努里数、欧拉数、费波那兹(L．Fibonacci)数都可用来研究第一情形。

探讨新的二阶递推序列对第一情形的应用，将是人们进一步研究的题目。

(5)人们也将探讨有力的研究第二情形的方法，以及其它的一些情形。在这些热点当中，前两个对费马大定理的彻底解决最富有探索性。

我们期待着人类在费马大定理上再创奇迹，早日攻克这一着名难题。

校稿附记：1993年6月23日，英国外尔斯(Andrew Wiles)在剑桥大学牛顿数学研究所作了两个半小时的题为“模形式，椭圆曲线和伽罗华表示”的学术报告，报告中宣布他证明了谷山－魏尔猜想对于半稳定的椭圆曲线成立。

由于费雷由费马方程的一组正整数解得到的椭圆曲线(称为费雷曲线)是半稳定的，并且费雷曲线不满足谷山－魏尔猜想，所以费马大定理已作为推论得到证明。

据英国报纸说，外尔斯的这项工作的预印本长达1000多页，目前完全弄懂这项工作的证明细节的数学家不会超过6人。所以，这项工作将需要几个月的时间进行审查。尽管如此，有关专家与权威人士仍大都持肯定态度。

笔者认为，不管结果如何，热点(1)～(5)仍将是有意义的课题，特别是给出简化的、简洁的或完全新的证明，仍将吸引数学家们的极大兴趣。

。【参考文献】：

1 Ribenboim P. 13 Lectures on Fermat's Last Theorem. New York: Springer-Verlag, 1980

2 Heath-Brown D R. Bull London Math,Soc,1985,17(1): 15～16

3 Adleman L M,Heath-Brown D R. Invent,Math, 1985,79 (2):409～416

4 Frey G.Ann UnivSarav Ser Math, 1986,1(1) :iv+40pp

5 曹珍富．自然杂志，1987，10(5)∶393；1989，12(9)∶718；1990，13(5)∶314

6 Silverman J H.J Number Theory, 1988,30:226～237

7 Granville A.Monagan M B. Trans Amer Math Soc. .1988, 306(1) :329～359

8 TannerJW,etal. Math Comp, 1989,53(188) :743～750

9 曹珍富．丢番图方程引论，哈尔滨：哈尔滨工业大学出版社，1989

10 Rotkiewicz A．Colloq Math，1991，62(1)∶15～19

(哈尔滨工业大学曹珍富教授撰)